Sums of Powers of Positive Integers - Solutions to Exercises 9-12

Exercise 9.

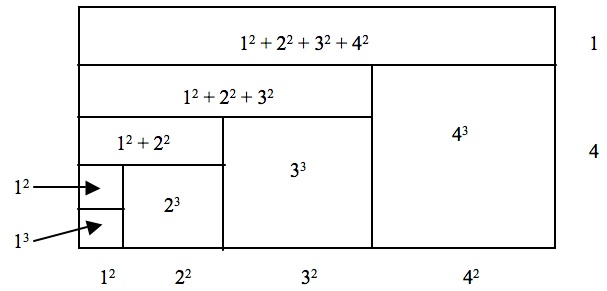
Figure 19. Each side of the equation $$(4 + 1)\sum_{i = 1}^4 {i^2 } = \sum_{i = 1}^4 {i^3 } + \sum_{p = 1}^4 {\sum_{i = 1}^p {i^2 } }$$ is the area of the rectangle.

Exercise 10. Let k = 1 in Figure 7. Then each side of the equation $$(n + 1)\sum_{i = 1}^n i = \sum_{i = 1}^n {i^2 } + \sum_{p = 1}^n {\sum_{i = 1}^p i }$$

is the area of the rectangle. Letting k = 1 in the equation $$(n + 1)\sum_{i = 1}^n {i^k} = \sum_{i = 1}^n {i^{k + 1}} + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}$$

gives the equation $$(n + 1)\sum_{i = 1}^n i = \sum_{i = 1}^n {i^2 } + \sum_{p = 1}^n {\sum_{i = 1}^p i }$$ or

$\displaystyle{(n + 1)(1 + 2 + 3 + \cdots + n) =}$ $$(1^2 + 2^2 + 3^2 + \cdots + n^2 ) + \sum_{p = 1}^n {(1 + 2 + 3 + \cdots + p)}$$ or

$\displaystyle{1^2 + 2^2 + 3^2 + \cdots + n^2 =}$ $$(n + 1)(1 + 2 + 3 + \cdots + n) - \sum_{p = 1}^n {(1 + 2 + 3 + \cdots + p)}$$ or $$\eqalign{1^2 + 2^2 + 3^2 + \cdots + n^2 & = (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - \sum_{p = 1}^n {{{p(p + 1)} \over 2}}\cr &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}\sum_{p = 1}^n {p^2 } - {1 \over 2}\sum_{p = 1}^n p \cr &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right)}$$

$\displaystyle{- {1 \over 2}\left( {1 + 2 + 3 + \cdots + n} \right)}$

or $$\eqalign{{3 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right) &= (n + 1)\left( {{{n(n + 1)} \over 2}} \right) - {1 \over 2}{{n(n + 1)} \over 2}\cr &= \left( {n + {1 \over 2}} \right)\left( {{{n(n + 1)} \over 2}} \right)}$$ or $$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n(n + 1)(2n + 1)} \over 6}.$$

Exercise 11. Let k = 2 in Figure 7. Then each side of the equation $$(n + 1)\sum_{i = 1}^n i^2 = \sum_{i = 1}^n {i^3 } + \sum_{p = 1}^n {\sum_{i = 1}^p i^2}$$

is the area of the rectangle. Letting k = 2 in the equation $$(n + 1)\sum_{i = 1}^n {i^k} = \sum_{i = 1}^n {i^{k + 1}} + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}$$

gives the equation $$(n + 1)\sum_{i = 1}^n i^2 = \sum_{i = 1}^n {i^3} + \sum_{p = 1}^n {\sum_{i = 1}^p i^2 }$$ or

$\displaystyle{(n + 1)(1^2 + 2^2 + 3^2 + \cdots + n^2 ) =}$ $$(1^3 + 2^3 + 3^3 + \cdots + n^3 ) + \sum_{p = 1}^n {(1^2 + 2^2 + 3^2 + \cdots + p^2 )}$$ or

$\displaystyle{1^3 + 2^3 + 3^3 + \cdots + n^3 =}$ $$(n + 1)(1^2 + 2^2 + 3^2 + \cdots + n^2 ) - \sum_{p = 1}^n {(1^2 + 2^2 + 3^2 + \cdots + p^2 )}.$$

If we now apply the formula for the sum of the squares, the equation becomes

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - \sum_{p = 1}^n {{{p(p + 1)(2p + 1)} \over 6}}$$ $$= (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - {1 \over 3}\sum_{p = 1}^n {p^3 } - {1 \over 2}\sum_{p = 1}^n {p^2 } - {1 \over 6}\sum_{p = 1}^n p$$

$$= (n + 1)\left( {{{n(n + 1)(2n + 1)} \over 6}} \right) - {1 \over 3}\left( {1^3 + 2^3 + 3^3 + \cdots + n^3 } \right)$$

$\displaystyle{- {1 \over 2}\left( {1^2 + 2^2 + 3^2 + \cdots + n^2 } \right) - {1 \over 6}\left( {1 + 2 + 3 + \cdots + n} \right)}.$

Collecting sums of cubes and applying the formula for the sum of the squares again, we have

$\displaystyle{{4 \over 3}\left( 1^3 + 2^3 + 3^3 + \cdots + n^3 \right) =}$ $$(n + 1)\left( {n(n + 1)(2n + 1) \over 6} \right) - {1 \over 2}{{n(n + 1)(2n + 1)} \over 6} - {1 \over 6}{{n(n + 1)} \over 2}$$ or $$\eqalign{1^3 + 2^3 + 3^3 + \cdots + n^3 &= {3 \over 4}\left( {{{n(n + 1)} \over {12}}\left( {2(n + 1)(2n + 1) - (2n + 1) - 1} \right)} \right)\cr &= {1 \over 4}\left( {{{n(n + 1)} \over 4}\left( {(2n + 1)^2 - 1} \right)} \right)\cr &= {1 \over 4}\left( {{{n(n + 1)} \over 4}\left( {4n^2 + 4n} \right)} \right)}$$ or $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left( n(n + 1) \over 2 \right)^2.$$

Exercise 12.

$$\eqalign{\left({n \over 5} + {1 \over 5} \right)n\left( n + {1 \over 2} \right)\left( (n + 1)n - {1 \over 3} \right) &={1 \over 5}(n + 1)n\left({1 \over 2} \right)(2n + 1)\left((n + 1)n - {1 \over 3} \right)\cr &={n(n + 1)(2n + 1) \over 6}\left({3 \over 5}(n + 1)n - {1 \over 5} \right).}$$