Sums of Powers of Positive Integers - Pythagoras (c. 570-500 BCE), Turkey-Greece-Italy

The Greek mathematician, philosopher, and mystic Pythagoras is said to have lived with his followers, the Pythagoreans, at Croton in what is now southern Italy. The Pythagoreans took as their motto “All is Number” and were believed to have experimented with number properties by arranging pebbles on a flat surface. As a result, they saw what we would describe as a sum of successive positive integers as a triangle or triangular number (Fig. 1).

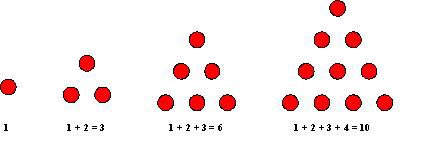
Figure 1. The first four triangular numbers

Their pebble experiments led them to see that two copies of the same triangular number could be fitted together to form an oblong number; hence, for example, twice the triangular number 15 = 1 + 2 + 3 + 4 + 5 could be viewed as the oblong number 5 x 6 = 30 (Fig. 2).

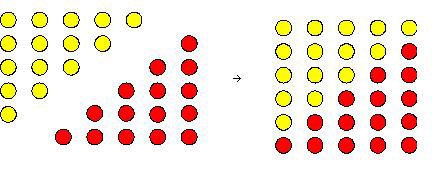
Figure 2. Twice a triangular number is an oblong number, or, in modern notation, \(2(1 + 2 + 3 + \cdots + n) = n(n + 1).\) Here we see that \(2(1 + 2 + 3 + 4 + 5) = 5\cdot 6.\)

Equivalently, any triangular number was half an oblong number; for example,

$$1 + 2 + 3 + 4 + 5 = {{5 \cdot 6} \over 2},$$

and, in general,

$$1 + 2 + 3 + \cdots + n = {{n(n + 1)} \over 2}$$

for any positive integer n.

Exercise 1: Use pebbles to illustrate that the sum of every two consecutive triangular numbers is a square number. Hint: Examples of pairs of consecutive triangular numbers include 6 and 10, 10 and 15, and 15 and 21.

The solution to this exercise is available here.