Sums of Powers of Positive Integers - Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (965-1039), Egypt

The mathematician and scientist Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (965-1039) was born in Basra in what is now southern Iraq, but spent most of his working life in Egypt.  He is most famous for his book Optics and specifically for the reflection problem named after him, “Alhazen’s Problem” (Katz, p. 256).

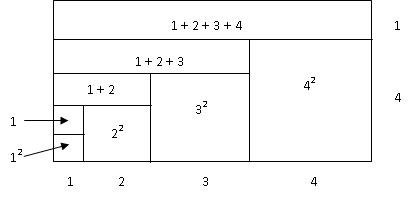
For his volume computations, al-Haytham needed formulas for the sums of the first n integer cubes and the first n fourth powers (C.H. Edwards, p. 83).  He may have used a diagram like that in Figure 6 (Baron, p. 70) to describe the relationship \[(4 + 1)\sum_{i = 1}^4 i  = \sum_{i = 1}^4 {i^2 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p i }.\]

Figure 6.  The area of this rectangle can be written in (at least) two different ways (after Baron, p. 70).

The area of the rectangle in Figure 6 can be written in (at least) two different ways.  Length times width gives area \[(4 + 1)(1 + 2 + 3 + 4),\] whereas adding together the areas of the eight regions gives area \[(1^2 + 2^2 + 3^2 + 4^2) + (1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4)).\]

Since each of these two expressions equals the area of the same rectangle, the two expressions are equal to one another.  Writing them using summation notation, we obtain the equation \[(4 + 1)\sum_{i = 1}^4 i  = \sum_{i = 1}^4 {i^2 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p i },\]

which can be solved for \[\sum_{i = 1}^4 {i^2 },\]

the sum of the first four squares.  Replacing 4 by n, we have the equation \[(n + 1)\sum_{i = 1}^n i  = \sum_{i = 1}^n {i^2 }  + \sum_{p = 1}^n {\sum_{i = 1}^p i },\]

which can be solved for \[\sum_{i = 1}^n {i^2 },\]

the sum of the first n squares.

The diagram in Figure 7 illustrates the more general relationship \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k } },\]

where each side of the equation gives the area of the rectangle (C.H. Edwards, p. 84). 

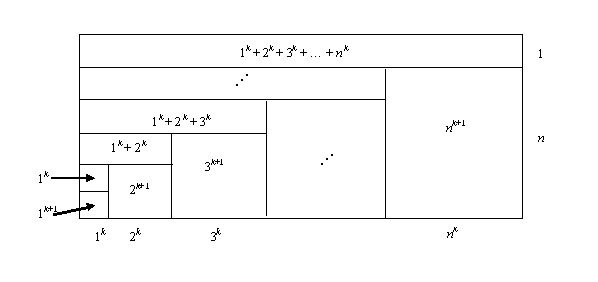
Figure 7.  The area of the rectangle in this figure, a generalization of Figure 6, can be written in (at least) two different ways (after C.H. Edwards, p. 84).

If we let k = 1 (see the preceding paragraph and Exercise 10) and use the formula \[1 + 2 + 3 +  \cdots  + n = {{n(n + 1)} \over 2},\]

we obtain \[1^2  + 2^2  + 3^2  +  \cdots  + n^2  = {{n(n + 1)(2n + 1)} \over 6}.\]

If we let k = 2 and substitute, using the formula for the sum of the squares, we obtain \[1^3  + 2^3  + 3^3  +  \cdots  + n^3  = \left( {{{n(n + 1)} \over 2}} \right)^2\]

(see Exercise 11).  If we let k = 3, we obtain \[(n + 1)\sum_{i = 1}^n i^3  =  \sum_{i = 1}^n {i^4 }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^3 } },\]

or

\(\displaystyle{(n+1)(1^3  + 2^3  + 3^3  +  \cdots  + n^3 ) =}\)

\[(1^4  + 2^4  + 3^4  +  \cdots  + n^4 ) + \sum\limits_{p = 1}^n {(1^3  + 2^3  + 3^3  +  \cdots  + p^3 )};\]

or

\(\displaystyle{1^4  + 2^4  + 3^4  +  \cdots  + n^4  =}\) \[(n + 1)(1^3  + 2^3  + 3^3  +  \cdots  + n^3 ) - \sum_{p = 1}^n {(1^3  + 2^3  + 3^3  +  \cdots  + p^3 )}\]

If we now apply the formula for the sum of the cubes, the equation becomes \[1^4  + 2^4  + 3^4  +  \cdots  + n^4  = (n + 1)\left( {{{n(n + 1)} \over 2}} \right)^2  - \sum_{p = 1}^n {\left( {{{p(p + 1)} \over 2}} \right)^2 }\]

\[ = (n + 1)\left( {{{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}} \right) - \sum_{p = 1}^n {\left( {{{p^4 } \over 4} + {{p^3 } \over 2} + {{p^2 } \over 4}} \right)} \]

\[ = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 4}\sum_{p = 1}^n {p^4 }  - {1 \over 2}\sum_{p = 1}^n {p^3 }  - {1 \over 4}\sum_{p = 1}^n {p^2 } \]

\[ = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 4}\left( {1^4  + 2^4  +  \cdots  + n^4 } \right) - {1 \over 2}\left( {1^3  + 2^3  +  \cdots  + n^3 } \right)\]

\(\displaystyle{{-\frac{1}{4}}\left(1^2 + 2^2  +  \cdots + n^2 \right).}\)

Collecting sums of fourth powers and applying the formulas for sums of cubes and squares, we have

\[{5 \over 4}\left( {1^4  + 2^4  +  \cdots  + n^4 } \right) = {{n^5 } \over 4} + {{3n^4 } \over 4} + {{3n^3 } \over 4} + {{n^2 } \over 4} - {1 \over 2}\left( {{{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}} \right)\]

\(\displaystyle{{-\frac{1}{4}}\left({\frac{n(n+1)(2n+1)}{6}} \right)}\)

or \[1^4  + 2^4  +  \cdots  + n^4  = {{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}\]

for all positive integers n.  Al-Haytham actually used n = 4 in his work, then stated the general result in words (Katz, pp. 256-257).  Translating al-Haytham’s words into our symbols, we have (Katz, p. 258) \[1^4  + 2^4  + 3^4  +  \cdots  + n^4  = \left( {{n \over 5} + {1 \over 5}} \right)n\left( {n + {1 \over 2}} \right)\left( {(n + 1)n - {1 \over 3}} \right)\]

for all positive integers n.
 

The righthand side of this equation is a multiple of \[{{n(n + 1)(2n + 1)} \over 6},\]

the sum of the first n positive integer squares, hence also of \[{{n(n + 1)} \over 2},\]

the sum of the first n positive integers.

Exercise 9:  Draw a rectangular figure like Figure 6 that illustrates the identity \[(4 + 1)\sum\limits_{i = 1}^4 {i^2 }  = \sum_{i = 1}^4 {i^3 }  + \sum_{p = 1}^4 {\sum_{i = 1}^p {i^2 } }.\]

Your rectangle will have height 5 and width 30.  Your figure need not be drawn to scale!

Exercise 10:  Draw a rectangular figure like Figure 6 or 7 that illustrates the identity \[(n + 1)\sum_{i = 1}^n {i = } \sum_{i = 1}^n {i^2 }  + \sum_{p = 1}^n {\sum_{i = 1}^p i }.\]

Provide the details of the computation that shows that letting k = 1 in the equation \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k } }\]

leads to the formula \[1^2  + 2^2  + 3^2  +  \cdots  + n^2  = {{n(n + 1)(2n + 1)} \over 6}.\]

Exercise 11:  Draw a rectangular figure like Figure 7 that illustrates the identity \[(n + 1)\sum_{i = 1}^n {i^2  = } \sum_{i = 1}^n {i^3 }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^2 }}.\]

Provide the details of the computation that shows that letting k = 2 in the equation \[(n + 1)\sum_{i = 1}^n {i^k  = } \sum_{i = 1}^n {i^{k + 1} }  + \sum_{p = 1}^n {\sum_{i = 1}^p {i^k }}\]

leads to the formula \[1^3  + 2^3  + 3^3  +  \cdots  + n^3  = \left( {{{n(n + 1)} \over 2}} \right)^2.\]

Exercise 12:  Show how to write al-Haytham’s formula \[\left( {{n \over 5} + {1 \over 5}} \right)n\left( {n + {1 \over 2}} \right)\left( {(n + 1)n - {1 \over 3}} \right)\]

for the sum of the first n fourth powers as a rational multiple of \[{{n(n + 1)(2n + 1)} \over 6}.\]

Solutions to these exercises can be found by clicking here.