Investigations Into d'Alembert's Definition of Limit: A Mini-Primary Source Project for Students of Real Analysis and Calculus 2

Author(s):

Dave Ruch (Metropolitan State University of Denver)

Students of mathematics struggle mightily with the meaning and definition of limit, whether in introductory courses on calculus or in real analysis. This seems fair, since mathematicians themselves have not always agreed on the subtleties of the concept, nor on the need to capture that concept in the form of a precise algebraic definition such as the one that we use today. A major problem in the development of today's definition was finding a useful bridge between the infinitesimal and finite worlds: how to translate ideas like "approach a limiting value" and "as close as we please" into precise algebraic inequalities with clear logical quantifiers. This mini-Primary Source Project (mini-PSP) explores the limit definition given and used by Jean-Baptiste le Rond d'Alembert (1717–1783).

Portrait of d'Alembert.
Convergence Portrait Gallery.

Early chapters of d'Alembert's biography read like something out of Masterpiece Theater. He was born out of wedlock and left as an infant at the church Saint Jean le Rond in Paris. His salonniére mother Claudine Guérin de Tencin never acknowledged him, and his father Louis-Camus Destouches found another woman to raise young Jean. Destouches died in 1726, but left funds for Jean's education. D'Alembert did well in school and became active as an adult in the philosophy, literature, science and mathematics of his day, standing "at the very heart of the Enlightenment with interests and activities that touched on every one of its aspects" [Hankins 1990]. He co-edited the quintessential work of the French Enlightenment, Diderot’s famous Encyclopédie, for a time, and wrote a number of its articles. Excerpts from two of these, “Limite” and “Calcul différential,” are used in the student project.

There are two versions of this mini-PSP: one for students of real analysis, and a more mild version for use in a first-year calculus course. D'Alembert's definition of limit has pedagogical value for modern students in both courses because it is reasonably close to a verbal version of our modern definition, but with two striking differences. In his 1754 article on the limit [d'Alembert 1754a], d'Alembert asserted (boldface added):

One says that a magnitude is the limit of another magnitude, when the second may approach the first more closely than by a given quantity, as small as one wishes, moreover without the magnitude approaching, being allowed ever to surpass the magnitude that it approaches;

......

Strictly speaking, the limit never coincides, or is never equal to the quantity of which it is the limit; but the latter approaches it ever more closely, and may differ from it by as little as one wishes. The circle, for example, is the limit of the inscribed and circumscribed polygons; for strictly it never coincides with them, though they may approach it indefinitely.

In other words, d'Alembert did not allow the converging quantity to ever reach or oscillate about the limiting value. Students are confronted with these differences in both versions of the project.

D’Alembert's original Encyclopédie article, “Limite.”
gallica.bnf.fr / Bibliothèque nationale de France.

Notably, d'Alembert's example in his 1754 article is sequential in nature, examining sequences of inscribed and circumscribed polygons converging to a circle. After an introduction with some historical background, the mini-PSP also focuses on the limit of a sequence. Some popular textbooks for real analysis treat sequential limits first, so the project can be used as an introduction to this core topic in either course. Proof-related ideas are omitted entirely from the Calculus 2 version of the mini-PSP, which focuses instead on basic examples of sequence convergence. In the real analysis version, students are guided from d'Alembert's verbal description of a sequence limit to a precise modern version using inequalities and quantifiers. That version further investigates two limit properties stated by d'Alembert: uniqueness of limits, and the convergence of a product of two converging quantities. D'Alembert gave a nice proof of the uniqueness result in his “Calcul différential” article, but using phrases such as "approach X as closely as we desire" and "the difference between Y and X can be as small as wished" [D'Alembert 1754b]. Students are asked to translate his theorem statements and give proofs of each in modern language.

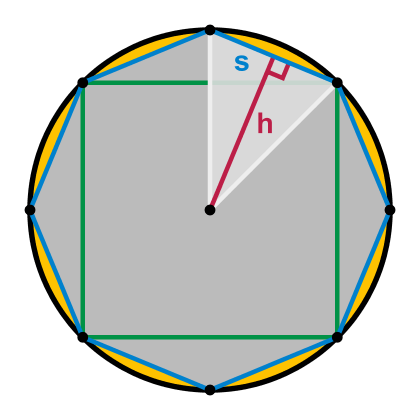
Octagon and square inscribed in circle, showing difference in perimeters.
Created by KSmrq [CC BY-SA (http://creativecommons.org/licenses/by-sa/3.0/)].

Both versions of the project Investigations Into d'Alembert's Definition of Limit are ready for student use, respectively subtitled Real Analysis Version (pdf file) and Calculus 2 Version (pdf file). The LaTeX source code of each is available from the author by request. A set of instructor notes offering background and practical advice for the use of the project in the classroom is appended at the end of both student versions of the project.

This project is the fourteenth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first-year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series appear below. The full TRIUMPHS collection includes twelve PSPs for use in a real analysis course, and seven PSPs for use in a Calculus 2 course.

Acknowledgments

The development of the student projects presented in this article has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation. The author gratefully acknowledges this support, with special thanks to TRIUMPHS PI Janet Heine Barnett, who helped with suggestions for producing the Calculus 2 version of the original project.

References

d’Alembert, Jean le Rond. 1754a. Limite (mathématiques). In Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, volume 9, page 542. Paris. Translation by Jacqueline Stedall, in Mathematics Emerging: A Sourcebook 1540–1900, pp. 297–298, Oxford: Oxford University Press, 2008.

d’Alembert, Jean le Rond. 1754b. Calcul différentiel. In Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, volume 9, pages 985–988. Paris. Translation by Gregory Bringman, in The Encyclopedia of Diderot & d’Alembert Collaborative Translation Project, Ann Arbor: Michigan Publishing, University of Michigan Library, 2003. https://quod.lib.umich.edu/d/did/did2222.0001.091.

Hankins, Thomas L. 1990. Jean d’Alembert: Science and the Enlightenment. New York: Gordon and Breach.

Dave Ruch (Metropolitan State University of Denver), "Investigations Into d'Alembert's Definition of Limit: A Mini-Primary Source Project for Students of Real Analysis and Calculus 2 ," Convergence (February 2020), DOI:10.4169/convergence20200301

Convergence

Tags:

History of Mathematics