L’Hôpital’s Rule: A Mini-Primary Source Project for Calculus 1 Students

Today it is well understood that calculus is organized around two central ideas, the derivative and the integral. It was not always this way. Neither of its “inventors,’ Isaac Newton (in the 1660s) nor Gottfried Leibniz (in the 1670s), conceived of their versions of the calculus as a way of producing from a given function a derivative function. This approach was pioneered by Joseph-Louis Lagrange more than 100 years later; he was the one who coined the term derivative, in his Théorie des Fonctions Analytiques (Theory of Analytic Functions) [1797]. Initially, Leibniz formulated his calculus by manipulating differentials: the differential \(dx\) was nothing more than a change in magnitude of the quantity \(x\); if another magnitude \(y\) changed as a result of the change in \(x\), its resulting increment, \(dy\), was the differential of \(y\). Leibniz then investigated the nature of the change by measuring the ratio of the differentials when these increments were “infinitely small.” But what did it mean to be “infinitely small”? Was that the same as “nothing”? If so, then how can we form ratios of these nothings? Lagrange, aware of this dilemma, intended to rewrite the calculus, specifically to remove its problematic foundation on the “infinitely small” differentials of Leibniz, but also to introduce another powerful idea that had been introduced by Leibniz and developed extensively by Leonhard Euler in the intervening decades, the concept of a function, the relation between the variable quantities being considered.

Newton’s original approach to the calculus was no less fraught: George Berkeley’s stinging critique of Newton’s fluxions as ratios of “evanescent increments” in his essay The Analyst [1734] captured mounting dissatisfaction with the underpinnings of Newton’s powerful calculus, a power sufficient to have successfully tamed the motions of the planets. Newton’s Principia Mathematica [1687] was highly respected for its mathematical explanation of the motions of the Sun on the planets and of the Earth on the Moon, and it was known that Newton’s fluxional calculus was at the heart of these theories. But Berkeley took Newton to task for how the calculus was established: “And what are these same evanescent Increments?” Berkeley accused mockingly in The Analyst. “They are neither finite Quantities, nor Quantities infinitely small, nor yet nothing. May we not call them the Ghosts of departed Quantities?” The metaphysical (foundational) struggle to establish what the calculus was really about would carry on well into the nineteenth century, especially through the work of Augustin-Louis Cauchy, who introduced limits into the foundations of calculus. Later, the work of Karl Weierstrass and Bernhard Riemann helped to carry the calculus forward into what we know today as the expansive field of analysis. But we don’t follow that road in this project.

Guillaume François Antoine, Marquis de l'Hôpital (1661–1704). Wikimedia Commons.

Instead, we note that the first applications of the calculus—beyond extending understandings of the physical world during the Scientific Revolution—were mostly in geometric problems: the finding of tangents to curves, of their curvature, of areas and volumes bounded by curves and surfaces. One such problem came to a nice and tidy resolution through the calculus of differentials, and it is known today as L’Hôpital’s Rule.

The French nobleman Guillaume François Antoine, Marquis de l'Hôpital was a devotee of the new mathematics of the Continental geometers at the turn of the eighteenth century, men such as Leibniz, Pierre Varignon, and the Swiss brothers Jakob and Johann Bernoulli. Having negotiated a commission for his services, L'Hôpital employed Johann Bernoulli over a period of a few months to instruct him in these new methods. The Marquis kept detailed notes of the lectures, and from these there emerged the first book-length account of the calculus. This work, Analyse des infiniment petits pour l'intelligence des lignes courbes [Analysis of the infinitely small, for the understanding of curved lines], was published in 1696 (and again in a posthumous second edition in 1715). The most well-known result from this work is a theorem that assisted in the determination of limits of indeterminate type \(\frac{0}{0}\). As L'Hôpital stated the problem,

Let [there] be a curved line such that the value of the ordinate \(y\) is expressed by a fraction, in which the numerator and the denominator each becomes zero when \(x = a \). . . . We ask what the value of the ordinate ought to be [when \(x = a\)]. . . . If we take the differential of the numerator and we divide it by the differential of the denominator, after having let \(x = a\), we will have the value that we wish to find for the ordinate. 

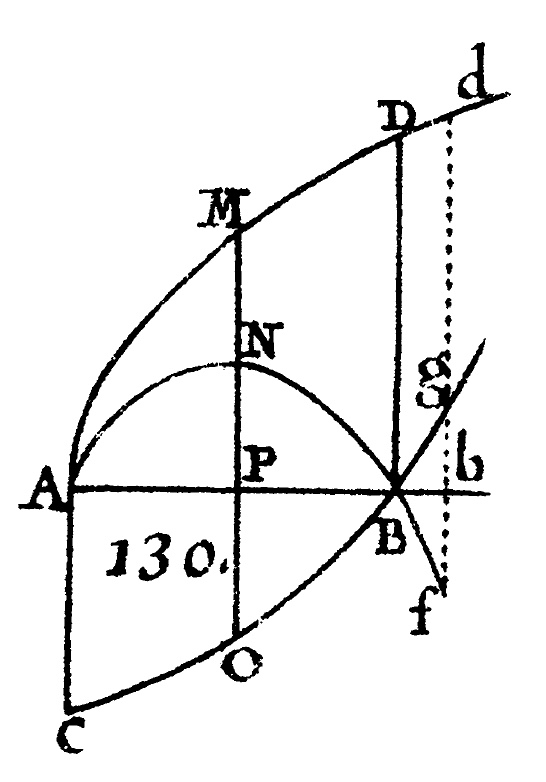
The intersecting curves \(ANBf\) and \(COBg\) in Figure 130 represent numerator and denominator curves
whose ratio produced the curve \(AMDd\) and an indeterminate form \(\frac{0}{0}\) at the point \(B\) [L’Hôpital 1715].

Students of calculus today learn this result as L’Hôpital’s Rule. But in a modern formulation, it is the quotient of derivatives, not the ratio of differentials, that resolves the problem. In the mini-Primary Source Project L’Hôpital’s Rule, students work through texts extracted from L’Hôpital’s Analyse, in which this proposition is stated in the language of differentials. The project is designed to help students not only to learn the Rule, but also to reinforce the idea of a derivative (here as the ratio of differentials) and to grapple with the subtle idea of the derivative as a limit of indeterminate type. An optional final section of the project focuses on formulating a proof of the Rule derived from L’Hôpital’s presentation. The project can be used by students who are seeing L’Hôpital’s Rule for the first time in the midst of an introductory calculus course, as well as by those later in their education who are looking back to review topics already introduced, such as students intending to teach calculus in secondary schools, or students looking for a capstone experience that deepens their understanding of calculus.

The complete project L’Hôpital’s Rule (pdf) is ready for student use, and LaTeX source code is available from the author by request. A set of instructor notes that explain the purpose of the project and guide the instructor through the goals of each of the individual sections is appended at the end of the student project.

This project is the thirty-third in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first-year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series appear below. " The full TRIUMPHS collection also offers thirteen additional mini-PSPs and four more extensive “full-length” PSPs for use in teaching calculus.

Acknowledgments

The development of the student project L’Hôpital’s Rule has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.

References

Baron, M. E. 1987. The Origins of the Infinitesimal Calculus. Dover Classics of Science and Mathematics. Mineola, NY: Dover Publications, Inc. First published in 1969 by Pergamon Press, Oxford, England.

Berkeley, G. 1734. The Analyst: A Discourse Addressed to an Infidel Mathematician: Wherein It Is Examined Whether the Object, Principles, and Inferences of the Modern Analysis Are More Distinctly Conceived, or More Evidently Deduced, Than Religious Mysteries and Points of Faith. Dublin: J. Tonson.

Boyer, C. B. 1959. The History of the Calculus and its Conceptual Development. Dover Books of Advanced Mathematics. New York: Dover Publications, Inc. First published in 1949 by Hafner Publishing Co. as The Concepts of the Calculus, A Critical and Historical Discussion of the Derivative and the Integral.

Lagrange, J.-L. 1797. Théorie des Fonctions Analytiques. Paris. Reprinted in Journal de l’Ecole Polytechnique, Cahier 9, Tome 3 (1801), 1–277. Second edition, 1813, third edition, 1847; both Paris: Bachelier. Also appears in Lagrange Oeuvres, Vol. 9, Paris: Gauthier-Villars, 1881.

L’Hôpital, G. F. A. d. 1715. Analyse des infiniment petits, pour l’intelligence des lignes courbes (Analysis of the infinitely small, for the understanding of curved lines). 2nd ed. Paris: Montalant.

Newton, I. 1687. Philosophiae Naturalis Principia Mathematica (The Mathematical Principles of Natural Philosophy). London: Royal Society.