Geometría Maya en la Sala de Clases: Proporciones Especiales en la Arquitectura Maya

Después de analizar muchas estructuras Maya clásicas y modernas e incluso participar en la construcción de algunos edificios Maya, Powell descubrió que varias proporciones especiales aparecen una y otra vez. Estas proporciones especiales incluyen las raíces cuadradas de los números enteros positivos hasta 5 y la proporción áurea \[\phi = {\frac{1+\sqrt{5}}{2}}.\]

Figure 4. Venta de flores a la salida de una iglesia en Chichicastenango, Guatemala.
Foto de Cynthia (Woodburn) Huffman, 2011.

(Para más información de la proporción áurea, vea la sección “Golden Ratio” del artículo Convergence “Leonardo of Pisa: Bunny Rabbits to Bull Markets.”) Los rectángulos cuyos lados están en estas proporciones se pueden construir fácilmente usando una cuerda de medir, que se explicará a continuación. En cada caso, primero se construye un cuadrado. Para diseñar una casa Maya típica, el cuadrado inicial tendría una longitud lateral de dos uinics [Powell, p. 39].

Powell ha teorizado que las flores son la respuesta a por qué los Mayas eligieron utilizar proporciones de raíces cuadradas y la medida áurea. Estas proporciones particulares surgen naturalmente en las flores, que eran, y siguen siendo, muy especiales para los Maya. Los Maya no cultivan flores, pero las flores silvestres son sagradas para ellos y, a menudo, las utilizan como ofrendas en ceremonias religiosas. Además, las flores y las conchas ocupan un lugar destacado en muchas obras de arte Maya clásicas. Pero la evidencia decisiva fue cuando un chamán maya moderno le dijo al Dr. Powell que su abuelo había dicho: “Las formas de las flores están en nuestras casas” [Powell, p. 116]. Para obtener detalles sobre la intrigante tesis de Powell, lo referimos a su disertación.

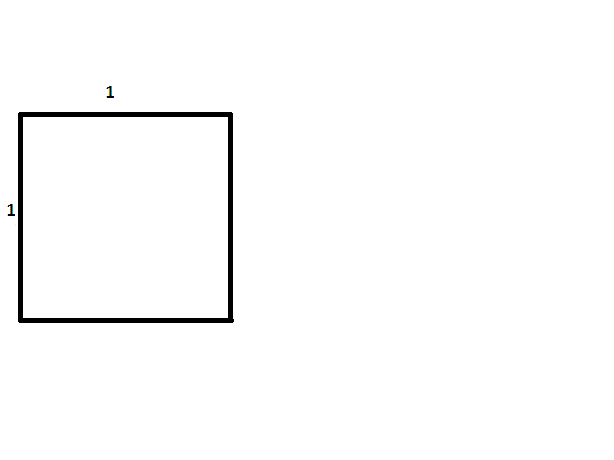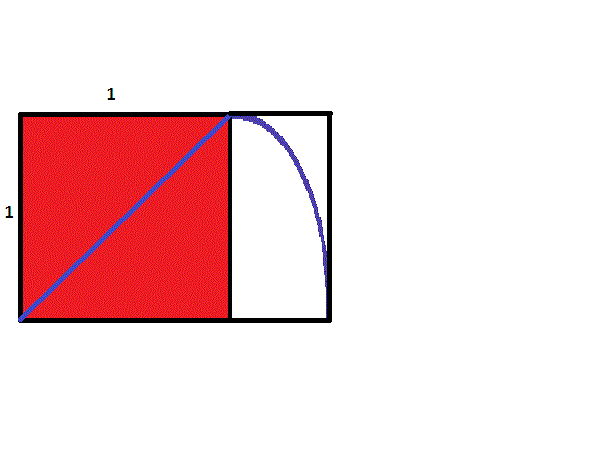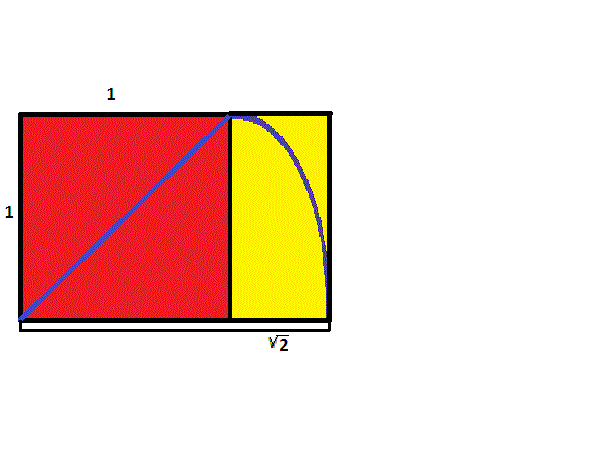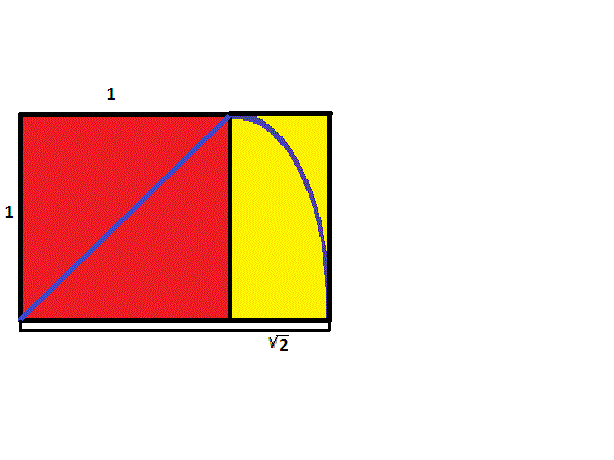
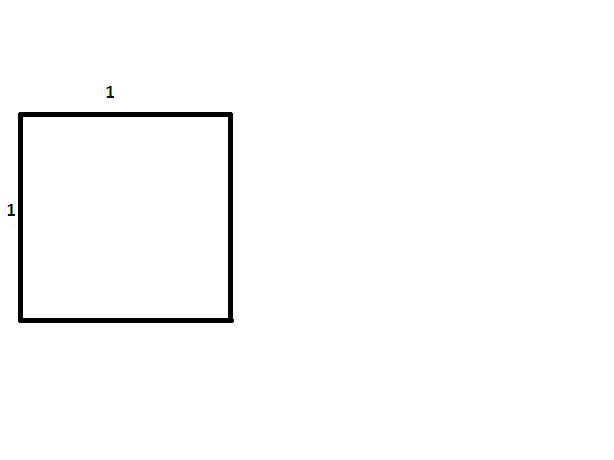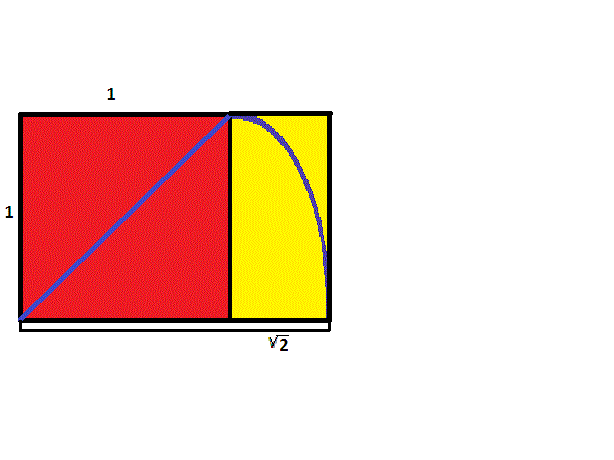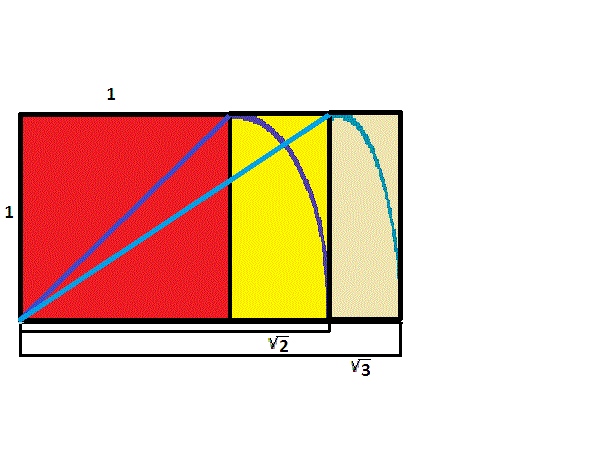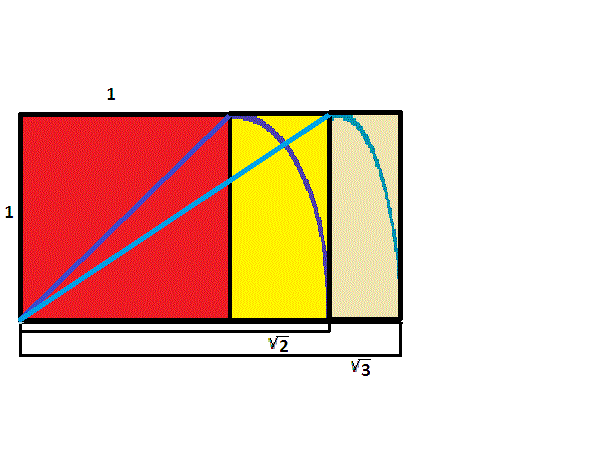
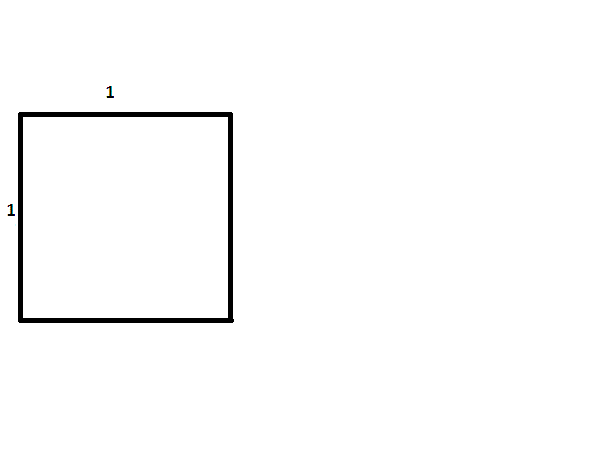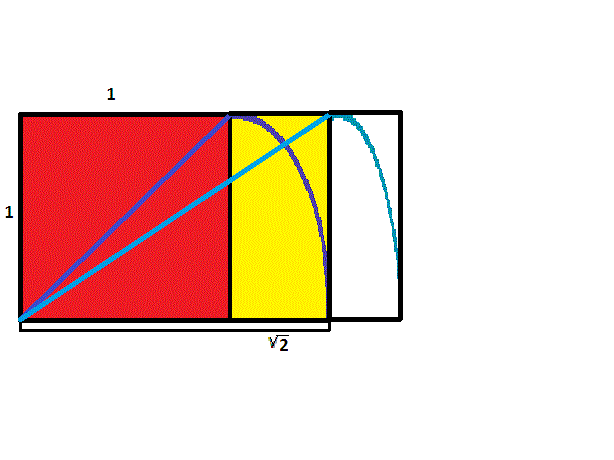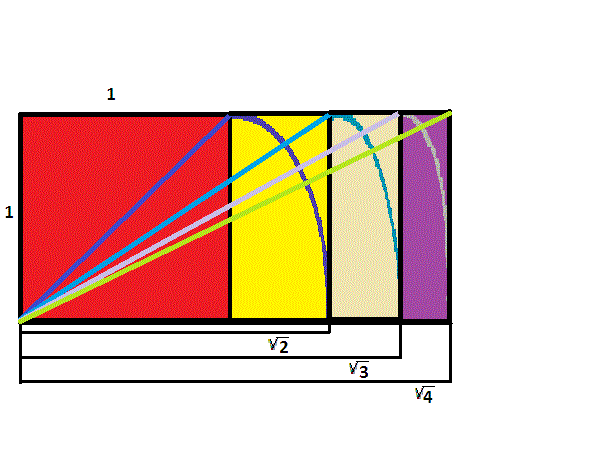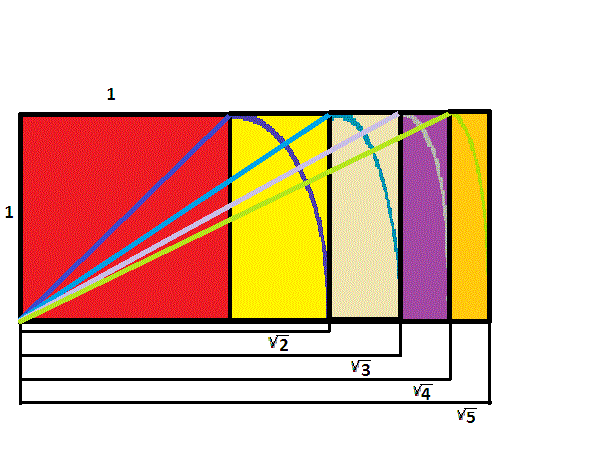
Para construir un rectángulo cuyos lados tengan una proporción de \(1\) a \({\sqrt{2}}\), comience con un cuadrado. Luego tome una cuerda y sujete un extremo en una esquina, estirándola hasta la esquina opuesta para formar una diagonal. Manteniendo la misma longitud que la diagonal y el primer extremo del cordón estacionario, balancee el otro extremo hasta que cruce la extensión de uno de los lados del cuadrado que contiene la primera esquina. Desde este punto de intersección, construya una perpendicular y continúe para construir un rectángulo que contenga el cuadrado original. Dado que el lado más largo tiene la misma longitud que la diagonal del cuadrado original, según el teorema de Pitágoras, la razón de los lados será  \({\sqrt{2}}\) a \(1\).

Si comenzamos con un rectángulo de lados en razón \({\sqrt{2}}\) a \(1\), y repetimos el mismo proceso de usar una cuerda para construir un rectángulo con un lado congruente a la diagonal, el resultado, usando el Teorema de Pitágoras, es un rectángulo con lados en razón \({\sqrt{3}}\) a \(1\).

El proceso continúa, permitiendo fácilmente construir rectángulos de lados en razón \({\sqrt{4}}=2\) a \(1\), y también \({\sqrt{5}}\) a \(1\).

Otra proporción que aparece con frecuencia en la arquitectura Maya es la proporción áurea \({\frac{1+\sqrt{5}}{2}}\). Para formar un rectángulo áureo usando un cordón, comience nuevamente con un cuadrado. Mida la longitud de un lado del cuadrado con una cuerda y dóblela por la mitad para marcar el punto medio de un lado del cuadrado. Luego, estire la cuerda desde este punto medio hasta una esquina opuesta y trace un arco para cruzar una extensión del lado del cuadrado donde se sostiene el otro extremo de la cuerda. Desde este punto de intersección, forme un rectángulo. La construcción se ilustra en la siguiente animación.

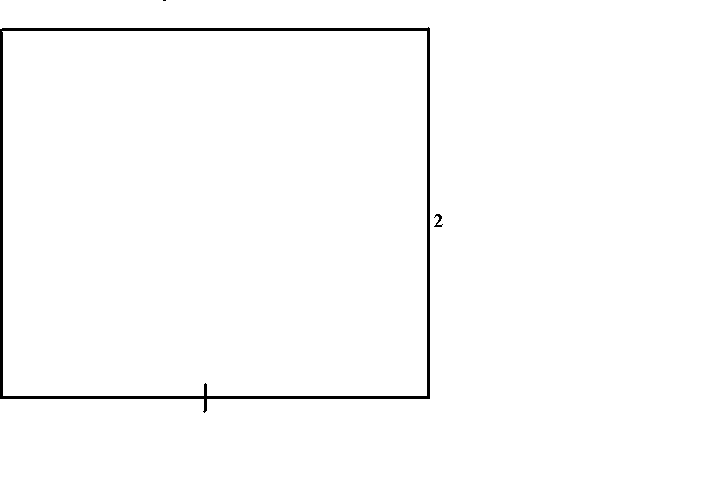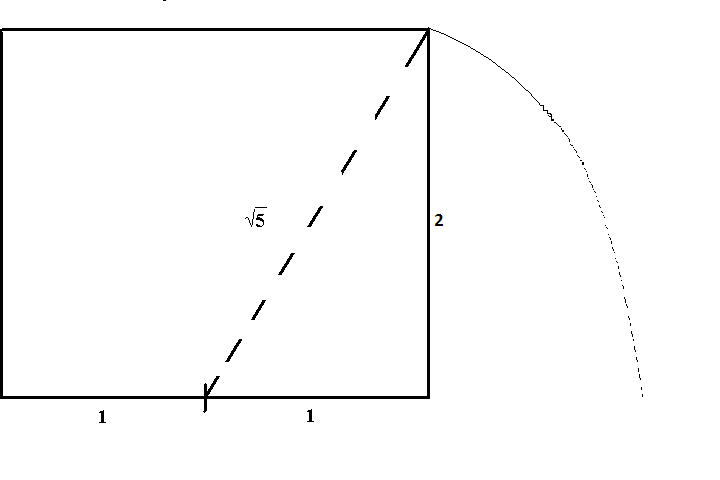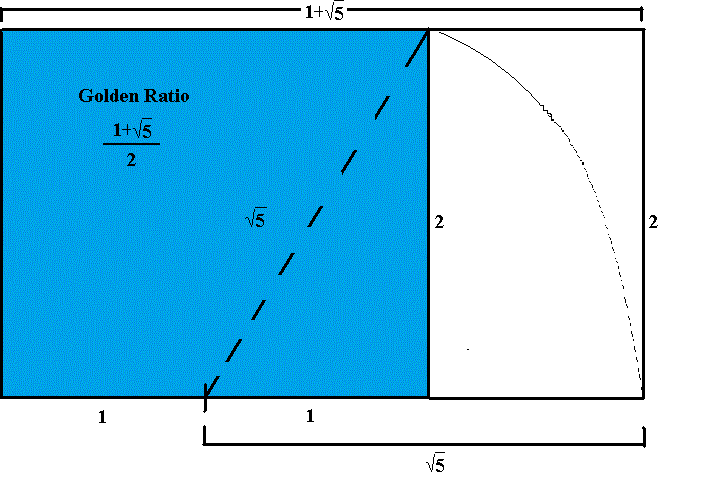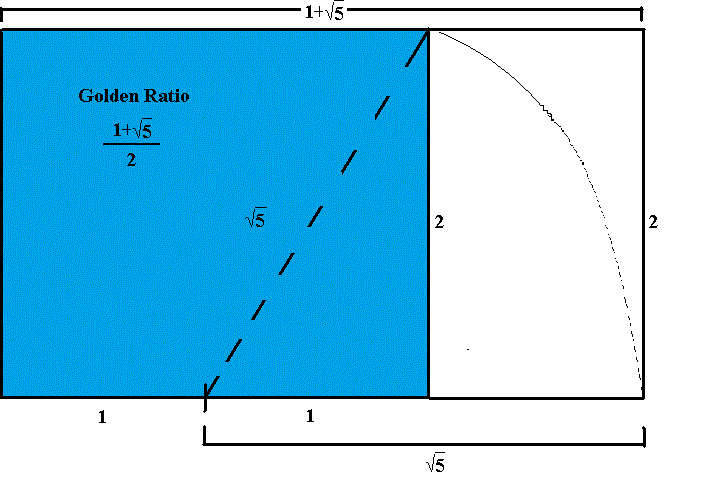
Para ver que el rectángulo construido es de hecho un rectángulo áureo, sin pérdida de generalidad, supongamos que el cuadrado inicial tiene una longitud de lado dos. Estire la cuerda desde el punto medio de un lado hasta una esquina opuesta para formar un triángulo rectángulo con lados de longitud \(1\) y \(2\). Según el teorema de Pitágoras, la hipotenusa tiene una longitud de \({\sqrt{5}}\). Entonces, el rectángulo resultante tiene un par de lados de longitud \(1+{\sqrt{5}}\) mientras que los otros lados tienen longitud \(2\). Por lo tanto, la proporción de los lados es la media áurea \({\frac{1+\sqrt{5}}{2}}\).

Muchas casas Maya, tanto antiguas como modernas, tienen una forma rectangular básica, pero con extremos redondeados. Estos también se pueden construir con la ayuda de cordones. Primero encuentre el punto medio de uno de los lados a redondear usando la cuerda, y luego estire la cuerda desde el punto medio hasta una esquina opuesta y gírela hacia la otra esquina. Luego repita el proceso en el otro lado del rectángulo.

Las Figuras 5 y 6 más abajo muestran casas Maya modernas construídas en estilo tradicional. Vea Everything Playa Del Carmen para información adicional y un video acerca de la construcción de “The Traditional House.”

Figura 5. Casas Maya en Campeche, México. Foto de Joel Haack, 2011; usada con permiso.

Figura 6. Casa Maya en Yucatán, México. Foto de Joel Haack, 2011; usada con permiso.