- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasures - Nicolo Tartaglia's Nova Scientia

This is the title page of the Nova Scientia (1537) of Nicolo Tartaglia (1499-1557). In this work, Tartaglia discussed the mathematics of artillery and developed methods for determining the range of a cannon. The caption below the illustration reads,
The Mathematical sciences speak: Who wishes to know the various causes of things, learn about us. The way is open to all.
The illustration itself depicts a walled compound, the compound of knowledge. The high wall keeps out the man who attempts to scale it and enter improperly. Entrance into the compound is through a single door opened by Euclid. In the first courtyard, a crowd comprised of Tartaglia and the muses of the seven liberal arts watch a demonstration of Tartaglia's new knowlege, a theory of trajectories. Beyond the first courtyard is a second smaller, more exclusive and highly elevated one. Its entrance is manned by Aristotle and Plato. Plato holds a banner proclaiming,
No one can enter who does not know geometry.
Enthroned at the rear of this compound, in the highest position of all, is philosophy.

Above: On this page (folio 29v), we see a method of determining the height of a distant object using a quadrant, or set-square.
Editor's note: The images above, from Columbia University Library's David Eugene Smith and George Arthur Plimpton collections, were posted on 5/14/2008. The images below, obtained through the courtesy of the Dibner Library of Science and Technology, Smithsonian Libraries, were added on 5/14/2017.
Tartaglia established that the trajectories of projectiles follow a (somewhat) parabolic path:
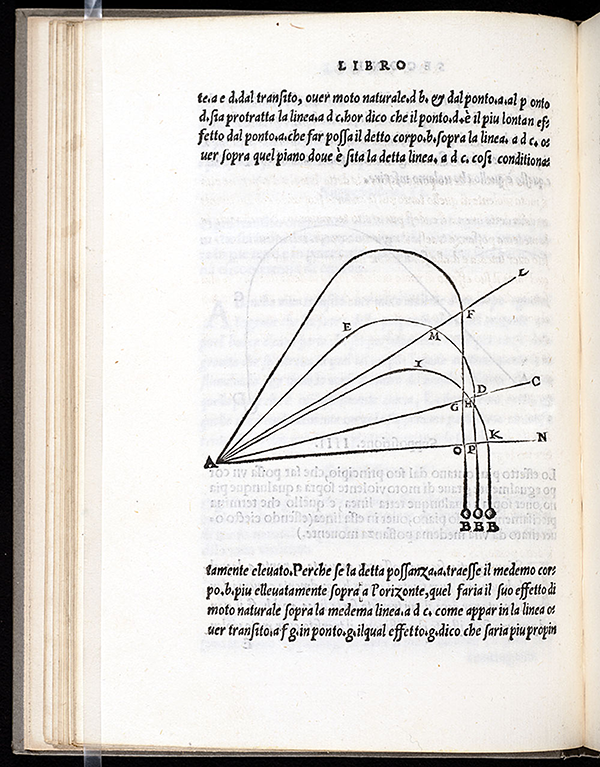
The range of a cannon is determined by the elevation of the barrel. Tartaglia designed a set-square, or quadrant, that would help gauge cannon barrel elevation:

Index to the Collection of Mathematical Treasures from the David Eugene Smith and George Arthur Plimpton collections, Columbia University Library
Index to the Convergence Collection of Mathematical Treasures
Frank J. Swetz and Victor J. Katz, "Mathematical Treasures - Nicolo Tartaglia's Nova Scientia," Convergence (January 2011)




