Mathematical Treasures - Albrecht Durer's Treatise on Mensuration

This is the page (30) illustrating the construction of an ellipse, from the Latin translation (1538) of the Treatise on Mensuration of Albrecht Dürer (1471-1528).  This book was originally written in German and published in 1525 and was designed to teach German artists the geometrical ideas on which perspective in painting was based.  On this page, Dürer shows how to construct an ellipse from its definition as a section of a right circular cone.  Unfortunately, Dürer did not get the curve quite right, presumably because he believed that it was wider at one end than the other.  (For more information on this, see Roger Herz-Fischler, "Dürer's Paradox or Why an Ellipse is Not Egg-Shaped," Mathematics Magazine 63 (1990), 75-85.)  

This page (33) illustrates Dürer's construction of a parabola, again by considering it as a section of a cone. 

T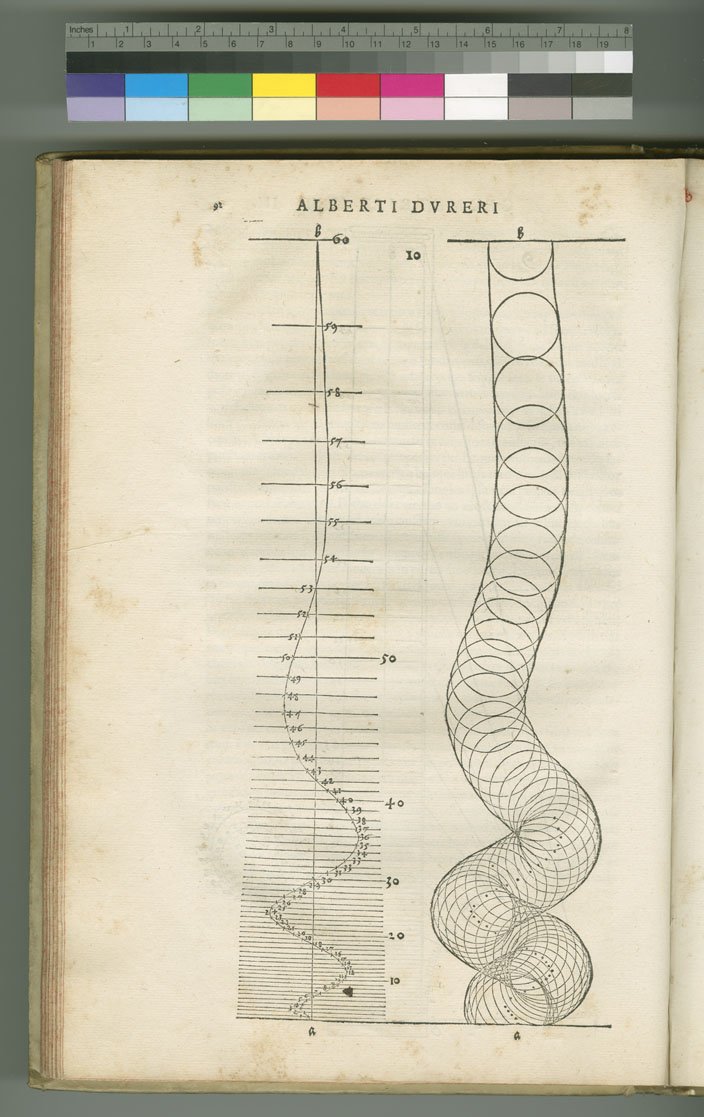

This page (92) illustrates the drawing of a spiral in space.

This woodcut print on page 185, called "The Designer of the Lute", illustrates how one uses projection to represent a solid object on a two-dimensional canvas.

Index to Mathematical Treasures