Kepler and the Rhombic Dodecahedron: The Rhombic Dodecahedron as a Cube with Pyramids – Volume as a Function of Edge Length

As we saw on a previous page, the volume of the rhombic dodecahedron is double the volume of the inscribed cube.

We now use this “double” relationship between the volume of the rhombic dodecahedron and the volume of the inscribed cube to write the volume of a rhombic dodecahedron as a function of its edge length.

First, recall (from our earlier computations) that if we start with a cube with side length 1, then each edge length of the rhombic dodecahedron is \(\frac{\sqrt{3}}{2}\). This lets us write the volume of this particular rhombic dodecahedron as a function of its edge length:

	Reveal answer.
	Hide answer.

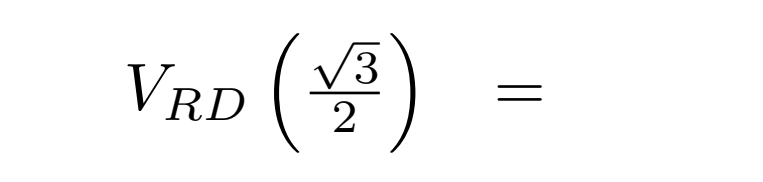Now, let’s scale this formula to get the volume of a rhombic dodecahedron that has edge length 1.

	Reveal answer.
	Hide answer.

	Reveal answer.
	Hide answer.

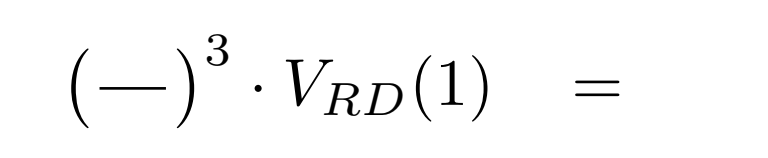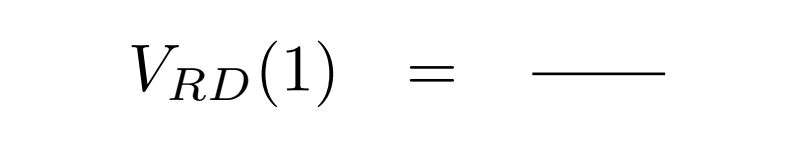Finally, we scale once more to get the volume formula for a rhombic dodecahedron with arbitrary edge length a.

	Reveal answer.
	Hide answer.

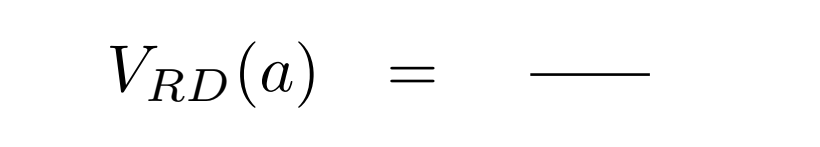Return to list of properties of the rhombic dodecahedron.