Kepler and the Rhombic Dodecahedron: The Rhombic Dodecahedron as a Cube with Pyramids – Some Basic Measurements

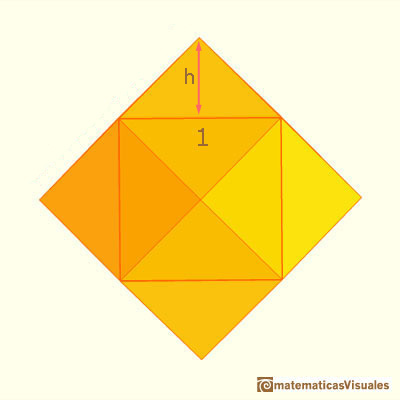
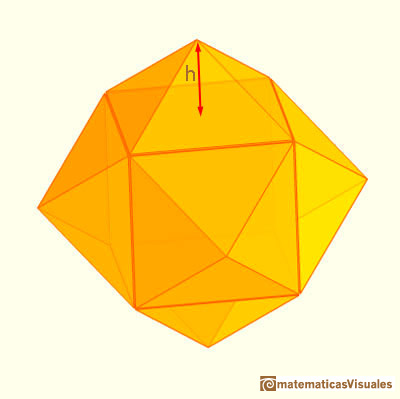
As was noted on the previous page, by viewing the rhombic dodecahedon as a cube augmented by pyramids, we can easily calculate some basic measurements; namely, the lengths of the diagonals of each face and the length of the polyhedron’s edges.

To do this, we need the precise height h of the raised pyramid that gives us the rhombic dodecahedron.

For simplicity, we can assume that the length of the cube’s edge is 1. The “trick” is then to slice through the three-dimensional object (shown at left below) to get a two-dimensional cross section (shown at right below). Elementary plane geometry and the Pythagorean Theorem let us calculate the value of h. Once you have found that value, click on the button below the cross-sectional image to see if you are correct.

	\(h=\)? \(h=\frac{1}{2}\)

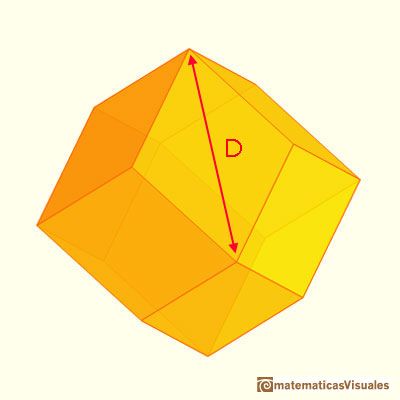
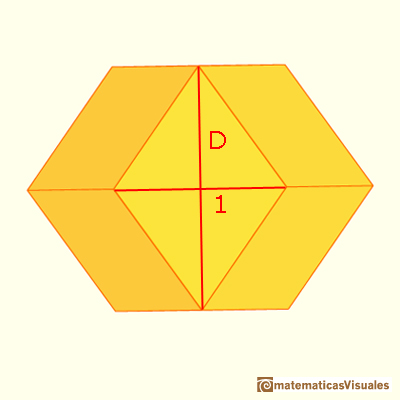
Looking again at the two images above, can you see how the side of the outer square of the cross section is the longer of the two diagonals of the rhombi that form the faces of our polyhedron? We can now calculate the length of the side of that outer square, which we label D in the next image. (The answer is once more hidden under the button):

\(D=\)? \(D=\sqrt{2}\)

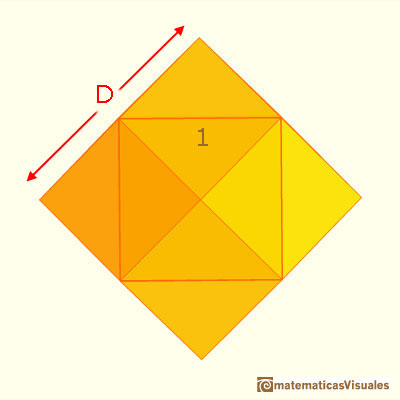As previously mentioned, our rhombi have two diagonals; the measure of the longer one is D . . .

. . . and the measure of the shorter one is 1 (by our initial assumption).

We can now use these values to calculate the side length of the rhombi, labeled a in the next diagram; this calculation also gives us the length of the polyhedron’s edges.

\(a=\)? \(a=\frac{\sqrt{3}}{2}\)

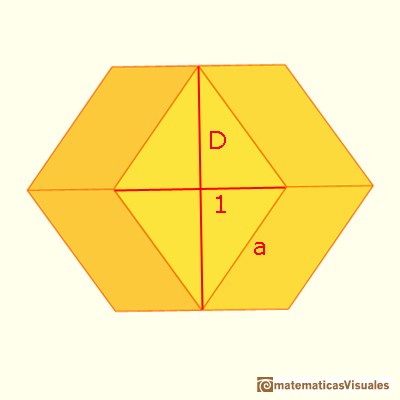And what if our initial cube doesn’t have unit length? Simply scale all the answers above by multiplying by the actual length of the cube’s edge! If you also know some basic trigonometry, you can find out about the angle measures with the following investigation.

Return to list of properties of the rhombic dodecahedron.