A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Khayyam's Geometric Demonstration

The construction gives instructions from which the reader can construct a segment that gives the solution to a polynomial of the form “cubes and squares and roots equal a number.” Because mathematical practice of the time insisted on maintaining dimensionality, it would only be possible to add terms with like dimension, so each term in the polynomial would essentially be viewed as a three-dimensional rectangular box. For Khayyam, then, finding the solution of a cubic was a geometrical question of finding the right sized line segment $\overline{LB}$ with which three boxes can be built so that their combined volumes equal a given volume. The first box is a perfect cube with volume $(LB)^3$. The second box has a square base of area $(LB)^2$ and given height $DB$. The third box has height $LB$ and given square base of area $(HB)^2$. The total volume of these three boxes must be equal to the given volume $(HB)^2 \times BG$. This condition generates the cubic equation $$(LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB = (HB)^2 \times BG$$ in $LB$ and Khayyam's construction yields a line segment ${\overline{LB}}$ whose length satisfies it.

Khayyam includes with the construction geometric reasoning to verify this claim. Below is a version of the proof that follows closely a translation of his presentation (Fauvel and Gray, pp. 233-234). This version outlines five key steps in the argument, with each step fully explained in turn. Below this geometric demonstration is then a suggestion for the reader to rework the argument in terms of contemporary algebraic notation, perhaps better to understand the relationship between the line segment $\overline{LB}$ and the polynomial $x^3 + ax^2 + b^2x = c^3$.

Step 1. First show that the areas of the rectangles $\square GLTK$ and $\square ZABL$ are equal.

Note that $\blacksquare ABCD$ indicates the area of the rectangle with vertices $A,$ $B,$ $C,$ and $D,$ and $\square ABCD$ denotes the rectangle itself.

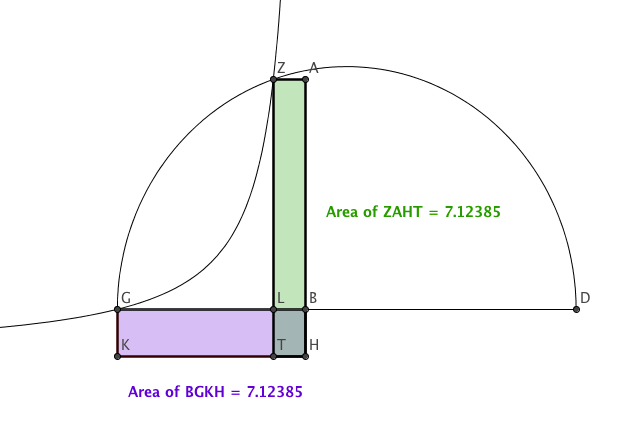
Figure 7. Since $\blacksquare ZAHT = \blacksquare GBHK$ and rectangles $\square ZAHT$ and $\square GBHK$ share $\square LBHT$, then the areas of the green and purple rectangles are equal. The above figure shows the area computation in the case of $x^3 + 7.9x^2 + 1.3^2 x = 2.1^3$.

Apollonius established a property of hyperbolas stating that the product of the distances from any point on the curve to each of the asymptotes is a constant. Since points $G$ and $Z$ are both on the same hyperbola with asymptotes $\overline{HK}$ and $\overline{HB}$, this means that the rectangles $\square ZAHT$ and $\square GBHK$ have the same area. Since these rectangles share the common rectangle $\square LBHT$, this means the difference rectangles $\square GLTK$ and $\square ZABL$ also have equal area as illustrated in Figure 7.

Step 2. Next, develop the ratio $\displaystyle\frac{(LZ)^2}{(GL)^2} = \frac{(HB)^2}{(LB)^2}.$

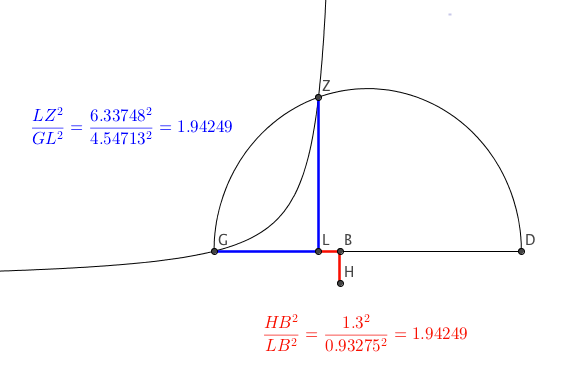
Figure 8. A computed example of equal ratios $\displaystyle\frac{(LZ)^2}{(GL)^2}$ and $\displaystyle\frac{(HB)^2}{(LB)^2}$ in the case of $x^3 + 7.9x^2 + 1.3^2 x = 2.1^3$.

Since we have equal areas $\blacksquare GLTK =$ $\blacksquare ZABL,$ this means that $(LZ) \times (LB) = (GL) \times (LT)$, so $\displaystyle \frac{LZ}{GL} = \frac{LT}{LB}.$ Since $HB$ is equal to $LT$, then $\displaystyle \frac{LZ}{GL} = \frac{HB}{LB}.$ Likewise, then, their squares will also be in proportion, which gives the ratio for Step 2.

Step 3. Then, use the semi-circle to obtain $\displaystyle \frac{(LZ)^2}{(GL)^2} = \frac{LD}{GL}.$

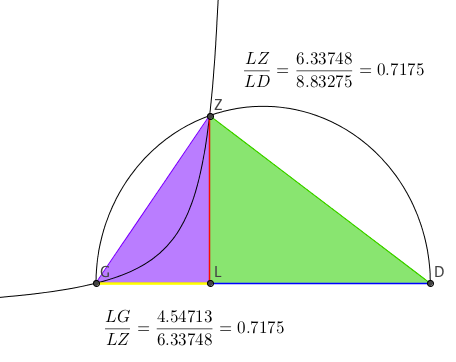
Figure 9. The green and purple triangles are similar. This yields the ratio $\displaystyle \frac{LG}{LZ} = \frac{LZ}{LD}$, which is necessary for Step 3.

Because triangle $\triangle DGZ$ is inscribed on the diameter in a semi-circle (as shown in Figure 9), it is a right triangle by Thales' Theorem. Then triangles $\triangle LGZ$ and $\triangle LDZ$ are also right triangles and, in fact, these three triangles are similar. Thus, we have $\displaystyle \frac{LG}{LZ} = \frac{LZ}{LD}$ which gives the necessary piece for our substitution: $\displaystyle (LZ)^2 = GL \times LD$. The equality for Step 3 follows directly.

Step 4. Next, demonstrate that $(HB)^2 \times GL = LD \times (LB)^2.$

Combine Steps 2 and 3 above for $\displaystyle \frac{(LZ)^2}{(GL)^2} = \frac{(HB)^2}{(LB)^2} = \frac{LD}{GL}.$ This means $(HB)^2\times GL = LD \times (LB)^2.$ Khayyam interpreted this as a geometric fact in terms of geometric solids, saying that the solid whose base is a square with sides of length of $HB$ and height $GL$ will have volume equal to a solid whose base is a square with sides of length $LB$ and height $LD$.

Step 5. Finally, verify that the length of the constructed segment $\overline{LB}$ satisfies the cubic.

Since point $B$ is between $D$ and $L$, then $LB$ + $DB$ = $LD$. This means we can divide the box with base of area $(LB)^2$ and height $LD$ into two smaller boxes: the cube with volume $(LB)^3$ plus a box with base of area $(LB)^2$ and height $DB$. This, combined with Step 4 above, gives $$(HB)^2 \times GL = LD \times (LB)^2 = (LB + DB) \times (LB)^2 = (LB)^3 + DB \times (LB)^2.$$ Now add to each side the volume $(HB)^2 \times LB$ to get $$(HB)^2 \times GL + (HB)^2 \times LB = (LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB.$$ Since $GL + LB = GB$, then $$(HB)^2 \times GB = (LB)^3 + DB \times (LB)^2 + (HB)^2 \times LB,$$ and $LB,$ the length of the constructed line segment ${\overline{LB}},$ solves the cubic.