A GeoGebra Rendition of One of Omar Khayyam's Solutions for a Cubic Equation - Combining Khayyam's Construction with a Modern Graph

Notably, Khayyam's construction generates a single line segment $\overline{LB}$ which solves the cubic equation of the form $x^3 + C_1x^2 + C_2x = C_3,$ where $C_1,C_2,C_3>0.$ In Figure 6 and Figure 7, for an example, we have fixed the coefficients to be $x^3 + 7.9x^2 + 1.3^2 x = 2.1^3,$ and in Figure 10, below, our example is $x^3 + 4.8x^2 + 1.4^2 x = 1.7^3.$ In Figure 10, we have reflected Khayyam's construction about the line $\overline{HB},$ the vertical asymptote of the hyperbola. Then, superimposing a Cartesian graph of a cubic shows clearly that $BL$ corresponds exactly to the positive root of the cubic.

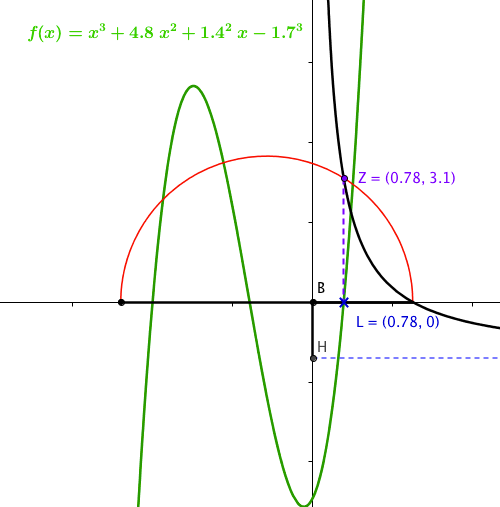
Figure 10. A reflection of Khayyam's construction for $x^3 + 4.8x^2 + 1.4^2 x = 1.7^3,$ superimposed with a Cartesian graph of the equivalent cubic function. We take line segment $\overline{HB},$ an asymptote for the hyperbola, as a vertical axis and line segment $\overline{BL}$ to have length $x$, which is exactly the value of a root to the cubic polynomial.

The slider bars in the GeoGebra applet in Figure 11 (below) enable students to explore how Khayyam's construction works for cubics with a range of coefficients. This dynamic exploration facilitates an appreciation of the general nature of the proof – Khayyam's method is not simply constructing one root to one specific polynomial. His construction technique constructs one root for any polynomial of the form $f(x) = x^3 + C_1x^2 + C_2x - C_3,$ where $C_1, C_2, C_3 > 0.$ The applet also presents in an accessible visual form the relationship between Khayyam's line segment $\overline{LB}$ and a root of the cubic graph familiar to many students.

Figure 11. A reflection of Khayyam's construction for $x^3 + ax^2 + b^2 x = c^3,$ with various positive values of $a,b,$ and $c,$ superimposed with a Cartesian graph of the equivalent cubic function. We take line segment $\overline{HB},$ an asymptote for the hyperbola, as a vertical axis and line segment $\overline{BL}$ to have length $x$, which is exactly the value of a root to the cubic polynomial.

In Figures 10 and 11, superimposing a Cartesian graph of a cubic shows clearly that $BL$ corresponds exactly to the positive root of the cubic. But what of the other roots?