A Euclidean Approach to the FTC - Appendix I: Proposition Six of Gregory's Geometry

Gregory's proof of the FTC is found in the proof of Proposition Six of the Universal Part of Geometry . In modern terms, if \(f(y)\) is a function (with graph \(BHNS\) in the figure below), the goal of this proposition is to construct a function \(g(y)\), whose arc length has the same ratio to its axis as the area under the graph of \(f(y)\) has to an inscribed rectangle with the same base. In other words, given \(f(y)\), the goal is to find a function \(g(y)\) such that

\({\textrm{arclength}(g(y)) \over y} = {\int_0^y f(t)\,dt \over c y}\)

where \(y\) is arbitrary and \(c\) is the length of the segment \(AB\), or

\(\int^y_0 \sqrt{ 1 + (g'(t))^2}\, dt = {1 \over c } \int_0^y f(t)\,dt\)

The FTC appears in the construction of the function \(g(y)\). First, he constructs a function \{h(y)\) via the defining equation \(f(y)^2 = c^2 +h(y)^2\). (In terms of the figure, \(AI = y\), \(IM = BA = c\), and \(h(y)\) is the curve \(AFLP\).) Then \(g(y)\), which has graph \(AKQ\), is defined by \(c g(y) = \int^y_0 h(t)\, dt\). The bulk of the proof is then devoted to showing that if \(\displaystyle c g(y) = \int^y_0 h(t)\,dt\), then \(c g'(y) = h(y)\), and this is precisely the FTC.

Proposition 6. Problem.

To find a curve which has the same ratio to its axis as any exhibited figure has to a rectangle inscribed in it and applied to a given line or axis of the sought-after curve.

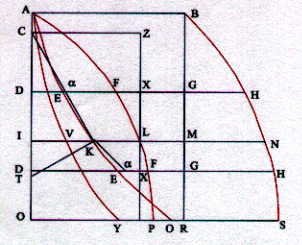
Let the exhibited figure be ABSO and let the inscribed rectangle be ABRO. Let the curve BS be simple or non-winding, but if it is not, the curve ought to be divided into many simple parts and the demonstration carried out separately. Next, let the curve AFLP be of such a nature that when any line IN is drawn normal to the line AO and cutting the curve AFLP in L, the square on IN will equal a sum of the squares of both IL and IM. Next, let the curve AEKQ be drawn of such a nature that when any line IM is drawn perpendicular to the line AO and cutting the curve AEKQ in K and AFLP in L, the rectangle MIK is equal to the curved region IAFL. I say that the figure ABSO is to the rectangle ABRO as the curve AEKQ is to the line AO.

For let K be a point on the curve AEKQ, through which is drawn the line IN perpendicular to the line AO and cutting the curves AFLP, BR, and BHNS in the points L, M, and N. Let IK be to IC as IL is to IM and let KC be drawn. The line KC either cuts or is tangent to the curve AQ in the point K. If possible, let it cut the curve at K and let it will fall within the curve at a point E toward the vertex A. Through the point E let a line DH be drawn parallel to IN and cutting AQ, AP, BR, and BS in the points E, F, G, and H, and the line KC in \(\alpha\). Also, complete the rectangle ILZC, whose side LZ cuts the line DH at X. Since IL is to IM as IK is to IC, the rectangle MIK—or the curved region IAFL—will be equal to the rectangle IZ. Since the rectangle GDE is equal to the curved region DAF, as IK is to DE thus will the curved region IAFL be to the curved region DAF. But IK has a greater ratio to DE than to D\(\alpha\). Thus, the curved region IAFL has a greater ratio to the curved region DAF than IK has to D\(\alpha\)—or IC has to DC. Therefore, the curved region IAFL has a greater ratio to the curved region DAF than the rectangle IZ has to the rectangle DZ, and, per conversionem rationis , the curved region IAFL has a smaller ratio to the curved region IDFL than the rectangle IZ has to the rectangle IX. By permuting, the curved region IAFL has a smaller ratio to the rectangle IZ than the curved region IDFL has to the rectangle IX. Since the rectangle IZ is equal to the curved region IAFL, the rectangle IX will be less than the curved region IDFL. But it is also more than the curved region IDFL, which is absurd. Consequently, the line KC does not fall within the curve AQ toward the vertex.

If possible, let the line CK fall within the curve toward the base, with the remaining things holding as in the previous situation. As IK is to DE, thus will the curved region IAFL be to the curved region DALF. But IK has a greater ratio to DE than to D\(\alpha\). Therefore, the curved region IAFL has a greater ratio to the curved region DALF than IK has to D\(\alpha\)—or IC has to DC. Therefore, the curved region IAFL has a greater ratio to the curved region DALF than the rectangle IZ has to the rectangle DZ. Through inverting, conversionem rationis , and inverting in turn, the curved region IAFL has a greater ratio to the curved region IDFL than the rectangle IZ has to the rectangle IX. By permuting, the curved region IAFL has a greater ratio the rectangle IZ than the curved region IDFL has to the rectangle IX. Since the curved region IAFL is equal to the rectangle IZ, the rectangle IX will be more than the curved region IDFL. But it is also less, which is absurd. Therefore, the line CK does not fall within the curve AQ toward the base. Thus, the line KC is tangent to the curve AQ in the point K.

Let the line KT, intersecting the line AO in T, be perpendicular to the line CK. It is manifest that CI is to CK as IK is to KT. But CI is to CK as MI is to NI, since the lines IN, IM, and IL are a right triangle similar to the triangle CIK, with sides IM and IN corresponding to the sides CI and CK. Consequently, as IK is to KT, thus is IM to IN. Since it is done in the same manner for all points of the curve AQ, it is manifest from Proposition Two that the line AO is to the curve AQ as the rectangle OB is to the figure ABSO, which it was desired to demonstrate.