Kepler and the Rhombic Dodecahedron: Conclusion – Kepler’s Other Rhombic Polyhedron Discovery

Kepler’s discovery of the rhombic dodecahedron by observing the base of bee cells marked the wonderful birth of a new polyhedron. He then showed that this rhombic dodecahedron was related to a technical problem: how best to pile up cannonballs. Next, he taught us perhaps the simplest way to understand the rhombic dodecahedron, as a cube augmented with pyramids. He also knew that the rhombic dodecahedron, like the cube, can be used to tessellate space.

Was his mind at rest following these discoveries? No, not at all.

Kepler wrote:

Intrigued by these rhombi [the rhombi from the bottom of bee cells], I began looking into geometry to see whether a body resembling the five regular solids and the fourteen^]7] Archimedean solids could be constructed exclusively from rhombi. I discovered two, one related to the cube and the octahedron, the other to the dodecahedron and the icosahedron. (The cube itself can be considered a third, since it is like two tetrahedra joined together.) The first of these solids is contained by twelve rhombi, the other by thirty [Kepler 1611, 43 and 45].

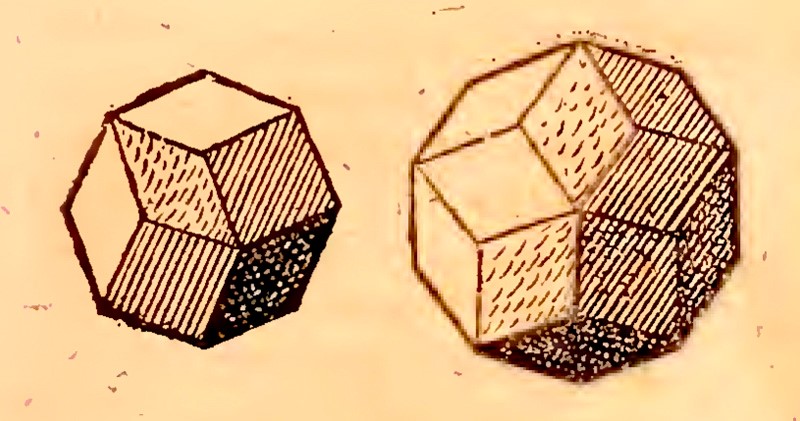
Figure 32. Drawings of a rhombic dodecahedron and a rhombic triacontahedron, from Harmonices Mundi Book II, p. 61.

The second rhombic polyhedron that Kepler discovered, with thirty faces, is called the triacontahedron.

Figure 33. Three rhombic polyhedra: rhombic dodecahedron, triacontahedron, and cube (3d-printed models).

How did Kepler discover the triacontahedron after identifying the rhombic dodecahedron?

What are the relations between these two rhombic polyhedra?

Is the cube a third rhombic polyhedron only because its six faces are square, that is to say, a special kind of rhombus? Or is there a deeper connection between these three rhombic polyhedra?

The study of the triacontahedron and the answers to these questions deserve another article!