A Euclidean Approach to the FTC - Gregory's Proof of the FTC

This Euclidean definition of the tangent is pivotal to Gregory's contradiction. For if \(KC\) is not tangent to \(OEK\), it means that some point \(\alpha\) on \(KC\) must lie above the curve \(OEK\). In particular, if \(DF\) is the line segment perpendicular to \(OA\) which intersects \(OA\) at \(D\), \(OEK\) at \(E\), \(KC\) at \(\alpha\), and \(OFL\) at \(F\), then \(DE < D \alpha\) by choice of \(\alpha\). This is shown in the figure below (adapted from Gregory's proof—see the Appendix).

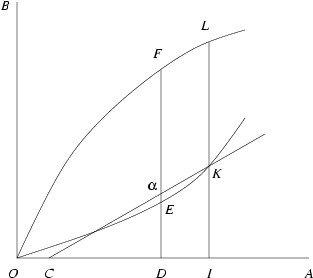
Actually, the figure tells only half of the story. It's also possible that a could lie on the other side of \(K\) on the line \(CK\). However, the argument for that case is similar, and the details make a good exercise (or see the Appendix).

By the definition of the curve \(OEK\), if \(\textrm{area}(OFD)\) denotes the area enclosed by the curve \(OF\) and the line segments \(OD\) and \(DF\), then \(DE = \textrm{area}(OFD)\). Likewise, \(IK = \textrm{area}(OFLI)\). Thus, \(IK/DE = \textrm{area}(OFLI)/\textrm{area}(OFD)\). Since \(DE < D \alpha\), it follows that \(IK/D \alpha < IK/DE\) and so

\({IK \over D\alpha } < {\textrm{area}(OFLI) \over \textrm{area}(OFD)}\)

This last step may seem mysterious, but it serves the purpose of converting the original inequality into an inequality about areas which will lead Gregory to an obvious geometrical contradiction. Specifically, \(DC \cdot IL\) is the area of the rectangle with sides \(IL\) and \(DC\), and \(IL \cdot IC\) is the area of the rectangle with sides \(IL\) and \(IC\). Inverting the ratios in the last inequality yields:

\({\textrm{area}(OFD) \over  \textrm{area}(OFLI)} < { DC \cdot IL \over  IC \cdot IL}\)

Now we can make some observations about these areas to arrive at a contradiction: Note that \(\textrm{area}(OFLI) = \textrm{area}(OFD) + \textrm{area}(DFLI)\) and likewise, since \(IC = DI + DC, IC \cdot IL = DI \cdot IL + DC \cdot IL\). Substituting these expressions into the numerators of the last inequality and doing some algebra, we have

\[{\textrm{area}(OFLI) - \textrm{area}(DFLI) \over \textrm{area}(OFLI)} < {IC \cdot IL - DI \cdot IL  \over  IC\cdot IL}\]

\[\iff\]

\[1 - {\textrm{area}(DFLI) \over \textrm{area}(OFLI)} < 1 -  { DI\cdot IL \over  IC\cdot IL }\]

\[\iff\]

\[{ DI \cdot IL \over IC \cdot IL } < { \textrm{area}(DFLI) \over \textrm{area}(OFLI)}.\]

But recall the defining equality for \(C\)—namely, \(IK/IC = IL\). This implies that \(IK = IC \cdot IL\). Since \(IK = \textrm{area}(OFLI)\) by definition of the curve \(OEK\), the denominators in the last inequality are the same. Therefore, the numerators must satisfy \(DI \cdot IL < \textrm{area}(DFLI)\). But remember that \(OFL\) is increasing by assumption. Thus, the rectangle with sides \(IL\) and \(DI\) must circumscribe the region \(DFLI\).

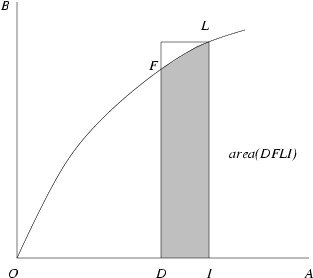
Hence \(\textrm{area}(DFLI) < DI \cdot IL\) as well. This contradiction shows that \(KC\) must in fact be tangent to \(OEK\). Hence the fundamental theorem of calculus follows.