Van Schooten's Ruler Constructions

Author(s):

C. Edward Sandifer

We repeat Problem I, trisecting a given angle.

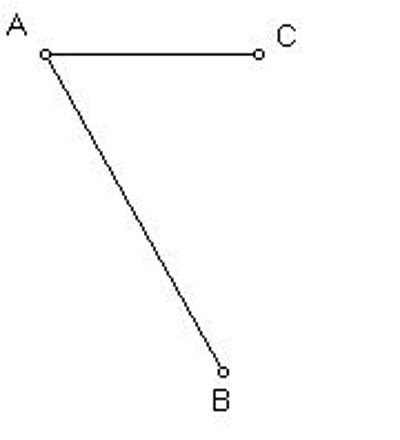
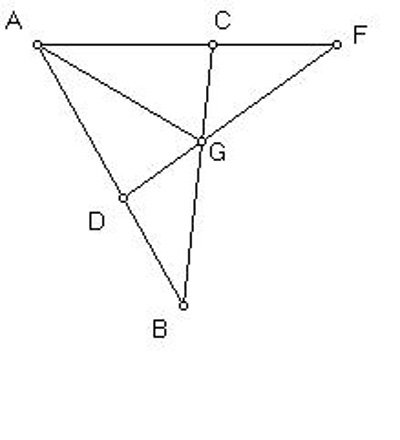
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.

The details of van Schooten's first solution to this problem are as follows.

Given the angle BAC,
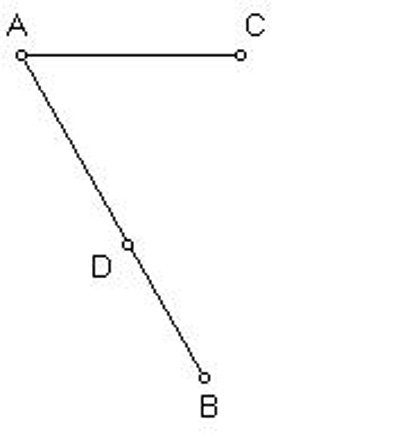
copy the segment AC onto the line AB to get the segment AD equal to AC.
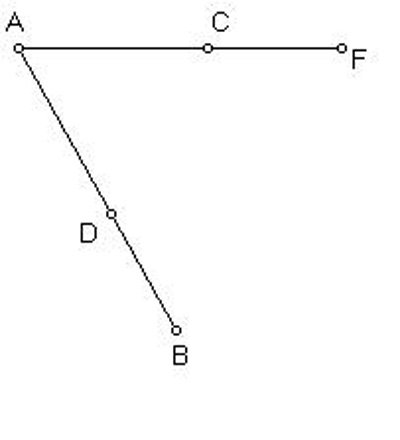
Likewise, copy the length AB onto the line AC, extended if necessary, to get the segment AF equal to AB.
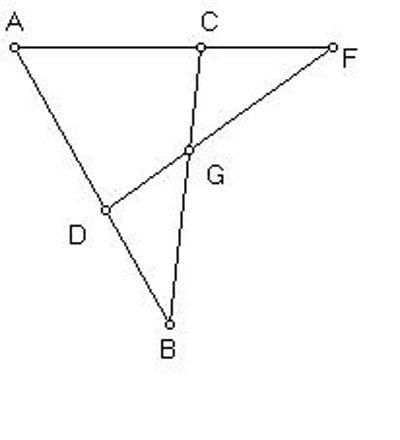
Now, draw the straight lines BC and DF, and let them intersect at the point G.
Now, the line AG will cut the angle into two equal pieces.

The sharp reader will notice that in this solution, we seem to assume that segment AC is shorter than segment AB. Though that can easily be circumvented, the solution will not quite work as given in the special case that AC equals AB. These issues do not seem to bother van Schooten at all.