- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Van Schooten's Ruler Constructions - Third Solution to Problem I
We repeat Problem I, trisecting a given angle.
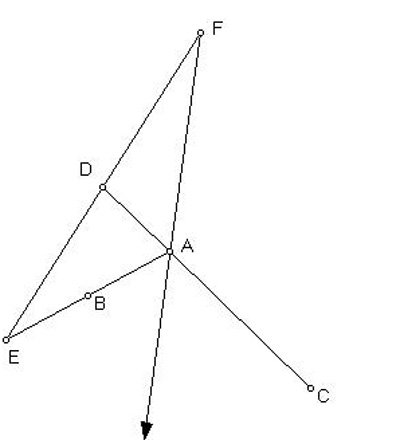
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
Van Schooten wrote a third solution.
And another way. Assume, as before, AD equals AB, that BD are joined, and that BE equals BA. And from E through D an indefinitely long straight line is drawn. In that, if DF is put, equal to DE, and from F through H [sic: should be A] is drawn FA: I say that this bisects the angle BAC.
Next:
C. Edward Sandifer, "Van Schooten's Ruler Constructions - Third Solution to Problem I," Convergence (August 2010)




