Maya Geometry in the Classroom: Special Ratios in Maya Architecture

After analyzing many classic and modern Maya structures and even participating in the construction of some Maya buildings, Powell discovered that several special ratios appear over and over again. These special ratios include square roots of the positive integers up to \(5\) and the golden ratio \[\phi = {\frac{1+\sqrt{5}}{2}}.\]

Figure 4. Flowers for sale outside a church in Chichicastenango, Guatemala.
Photo by Cynthia (Woodburn) Huffman, 2011.

(For more information on the golden ratio, see the “Golden Ratio” section of the Convergence article “Leonardo of Pisa: Bunny Rabbits to Bull Markets.”) Rectangles whose sides are in these ratios can easily be constructed by use of a measuring cord, which will be explained below. In each case, a square is first constructed. To lay out a typical Maya home, the initial square would have a side length of two uinics [Powell, p. 39].

Powell has theorized that flowers are the answer to why the Maya chose to use ratios of square roots and the golden mean. These particular ratios arise naturally in flowers, which were, and still are, very special to the Maya. The Maya do not cultivate flowers but wildflowers are sacred to them and often used as offerings in religious ceremonies. Also, flowers and shells are displayed prominently in many classic Maya artworks. But the deciding evidence was when a modern Maya shaman told Dr. Powell that his grandfather had said, “The shapes of the flowers are in our houses” [Powell, p. 116]. For details about Powell's tantalizing thesis, we refer you to his dissertation.

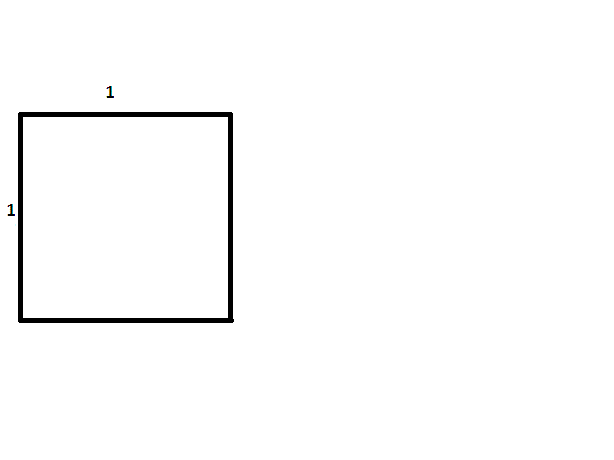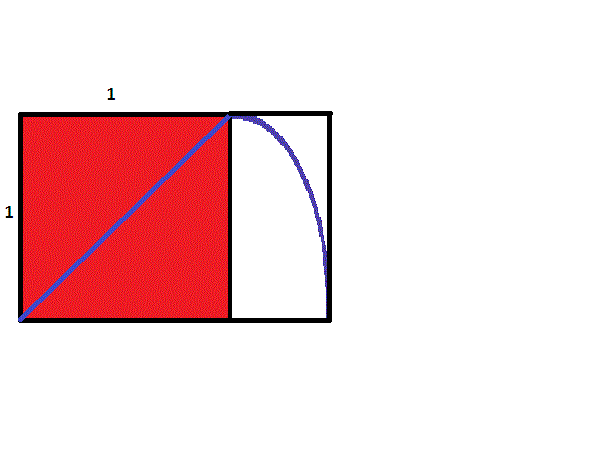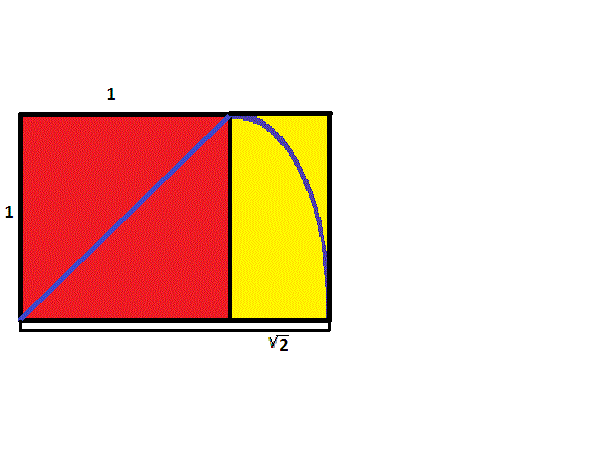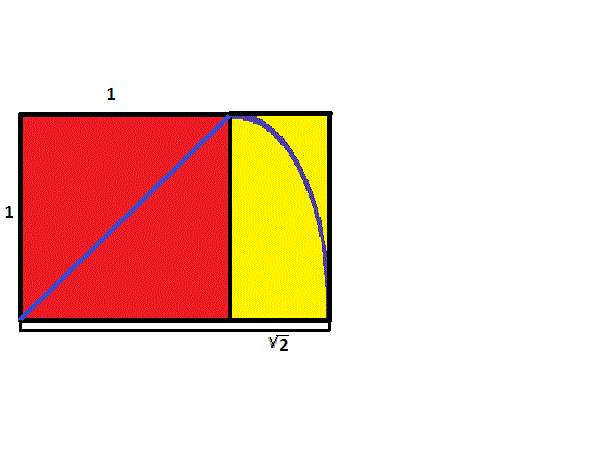
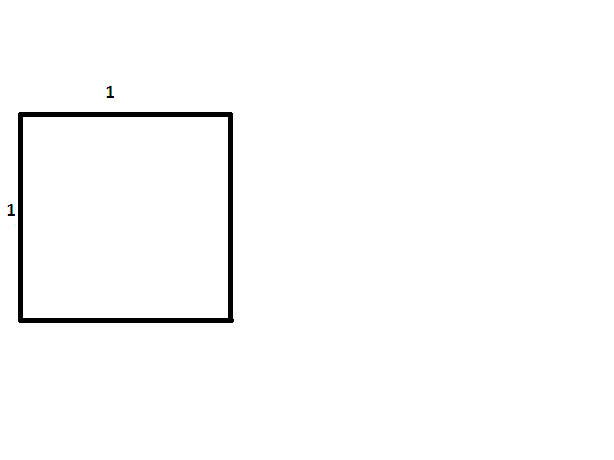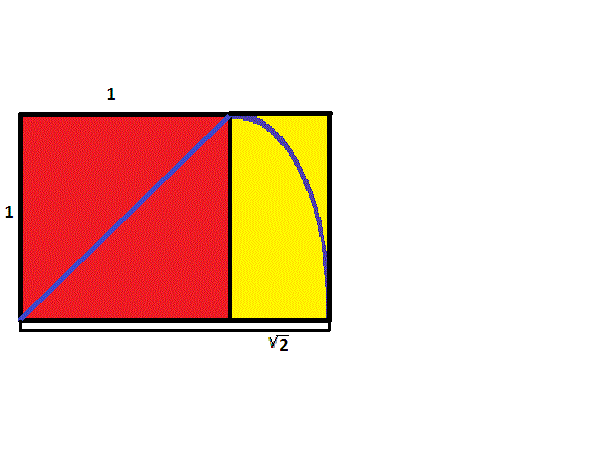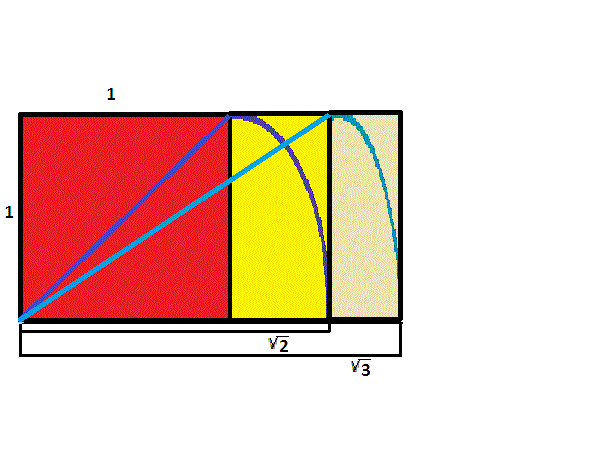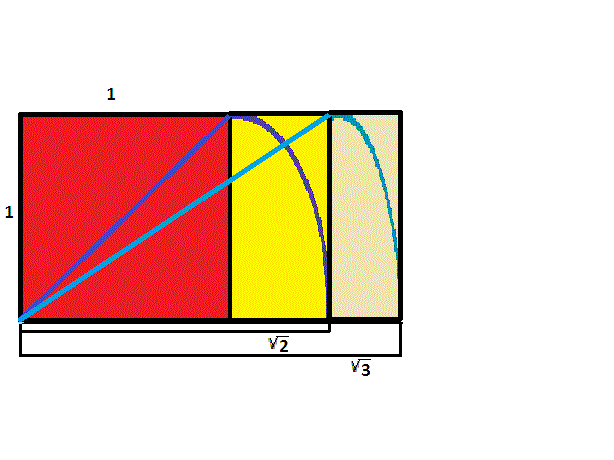
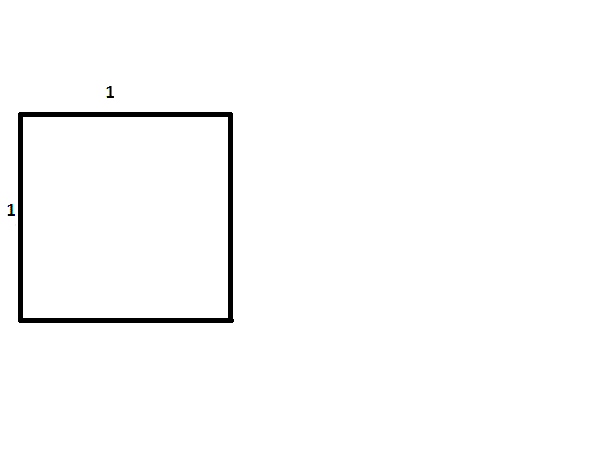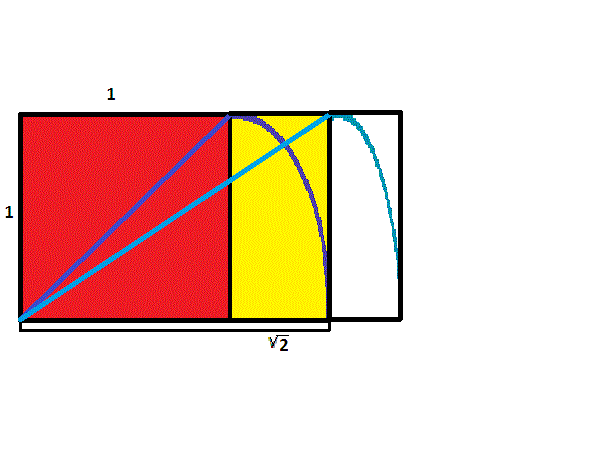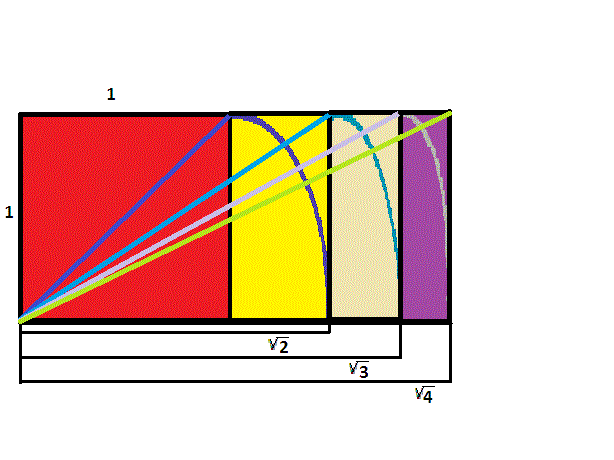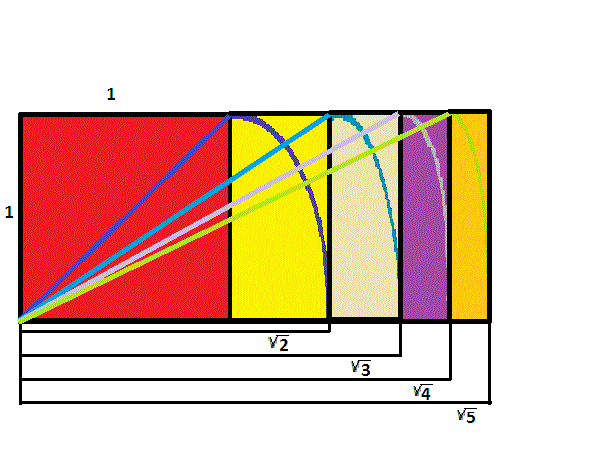
To construct a rectangle whose sides are in ratio of \(1\) to \({\sqrt{2}}\), start with a square. Then take a cord and hold one end at one corner, stretching to the opposite corner to form a diagonal. Keeping the length the same as the diagonal and the first end of the cord stationary, swing the other end until it intersects the extension of one of the sides of the square containing the first corner. From this intersection point, create a perpendicular, continuing on to construct a rectangle containing the original square. Since the longer side has length the same as the diagonal of the original square, by the Pythagorean Theorem, the ratio of the sides will be \({\sqrt{2}}\) to \(1\).

If we start with a rectangle with sides in ratio of \({\sqrt{2}}\) to \(1\), and repeat the same process of using a cord to make a rectangle with a side congruent to the diagonal, the result, again by the Pythagorean Theorem, is a rectangle with sides in ratio of \({\sqrt{3}}\) to \(1\).

The pattern continues, allowing one to easily construct rectangles with sides in ratio of \({\sqrt{4}}=2\) to \(1\), as well as \({\sqrt{5}}\) to \(1\).

Another ratio that appeared frequently in Maya architecture is the golden ratio \({\frac{1+\sqrt{5}}{2}}\). To form a golden rectangle using a cord, again start with a square. Measure the length of a side of the square with a cord and fold in half to mark the midpoint of a side of the square. Then stretch the cord from this midpoint to an opposite corner and swing an arc to intersect an extension of the side of the square where the other end of the cord is held.  From this intersection point, form a rectangle. The construction is illustrated in the animation below.

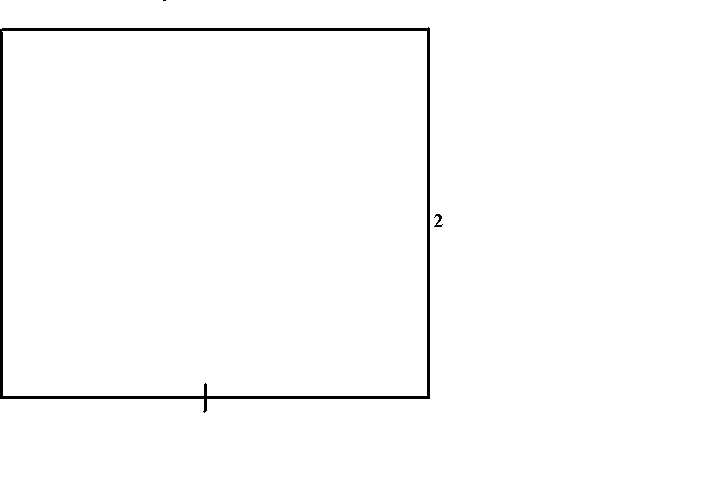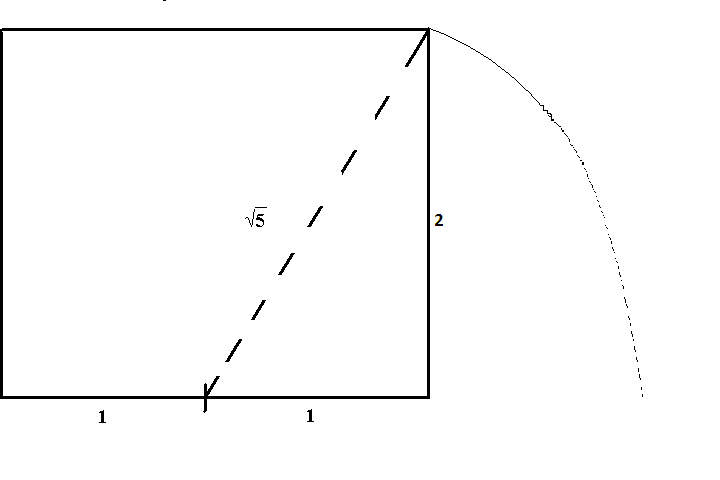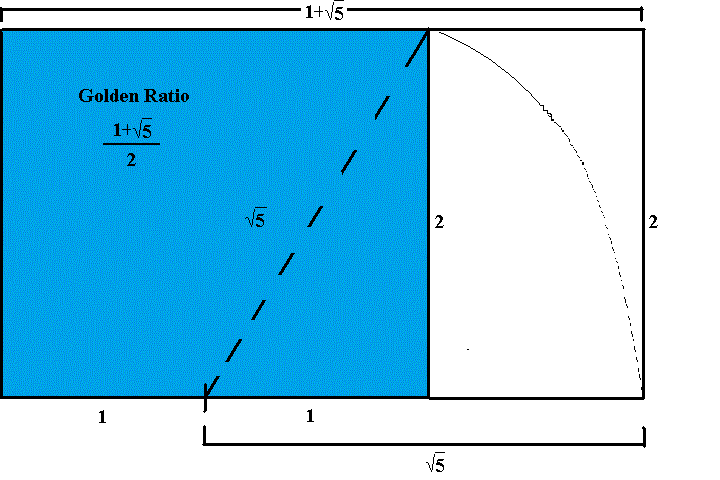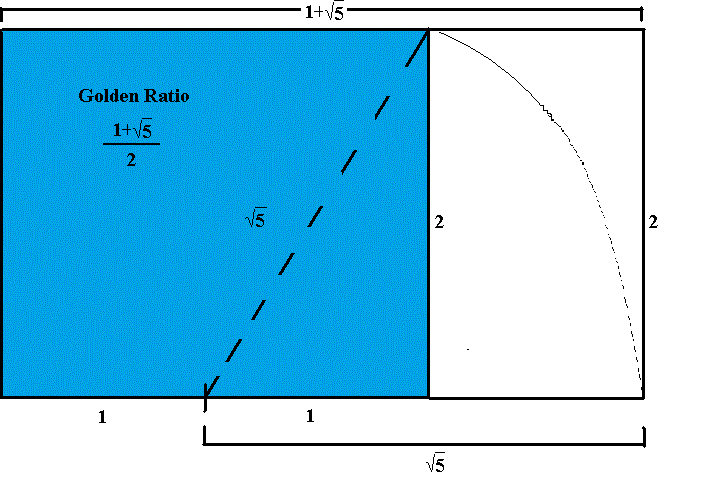
To see that the constructed rectangle is indeed a golden rectangle, without loss of generality, suppose the initial square has side length two. Stretching the cord from the midpoint of a side to an opposite corner forms a right triangle with side lengths \(1\) and \(2\).  By the Pythagorean Theorem, the hypotenuse has length \({\sqrt{5}}\). So, the resulting rectangle has one pair of sides of length \(1+{\sqrt{5}}\) while the other sides are length \(2\).  Hence, the ratio of sides is the golden mean \({\frac{1+\sqrt{5}}{2}}\).

Many Maya houses, both ancient and modern, have a basic rectangular shape, but with rounded ends. These also can be constructed with the help of a cord. First find the midpoint of one of the sides to be rounded by using the cord, and then stretch the cord from the midpoint to an opposite corner and swing the cord to the other corner. Then repeat the process on the other side of the rectangle.

Figures 5 and 6 below show modern Maya houses built in the traditional style. See Everything Playa Del Carmen for additional information and a video about the construction of “The Traditional House.”

Figure 5. Maya houses in Campeche, Mexico. Photo by Joel Haack, 2011; used with permission.

Figure 6. Maya house in Yucatan, Mexico. Photo by Joel Haack, 2011; used with permission.