Mabel Sykes: A Life Untold and an Architectural Geometry Book Rediscovered – Sykes’ 1906 Persian Arch Construction

Before we present Sykes’ architectural constructions, it will be helpful to review some basic geometric constructions. The Euclidean tools of construction are limited to an unmarked straightedge and a compass. We can visualize the straightedge as a ruler without markings for length. The compass is the tool that allows us to construct a circle by planting one compass point while sweeping the other. We will assume that we have a rigid compass, that is, given a point, A, and a segment of length r, we can construct the circle with center \(A\) and radius \(r\). With these tools we are able perform a number of standard constructions, including:

• Constructing an equilateral triangle given a segment as a side [I.1]¹
• Bisecting a given angle [I.9]
• Bisecting a given segment [I.10]
• Constructing a perpendicular to a line from a point on the line [I.11]
• Constructing a perpendicular to a line from a point not on the line [I.12]
• Copying an angle [I.23]
• Constructing a parallel to a line from a point not on the line [I.31]
• Dividing a given segment into n equal segments [VI.9]

We now take a look at one of Sykes’ earlier constructions, taken from her article “Some Practical Applications of Elementary Geometry,” which she began by commenting, “The mind ... must be trained to effective doing through the solution of practical problems” [29]. For her first example of a real-world problem from mechanical drawing she gave the construction of a particular type of ogee arch called a Persian arch. An ogee arch consists of two ogee curves meeting at an apex. An ogee curve bears a resemblance to the letter S in that it consists of two arcs of opposite concavity. Three ogee arches are found in the close-up image of the Yorkshire church shown in Figure 4. The largest ogee arch appears above the large central window, the smallest is found above the door on the lower right, and another is found above the main entrance door.

Figure 4: Beverley Minster in Yorkshire, England. Wikimedia Commons.

In her Source Book that appeared six years after this article, Sykes presented the constructions of four other types of ogee arches and provided some historical and architectural context:

The ogee arch is much used on Turkish buildings, and is common as an ornamental feature in the late Gothic. It is very generally used in canopies and gables in the masses of ornament that cover the inside and outside of the later Gothic cathedrals. Half of it is sometimes used for veranda rafters, and for roofs of bay and oriel windows [40].

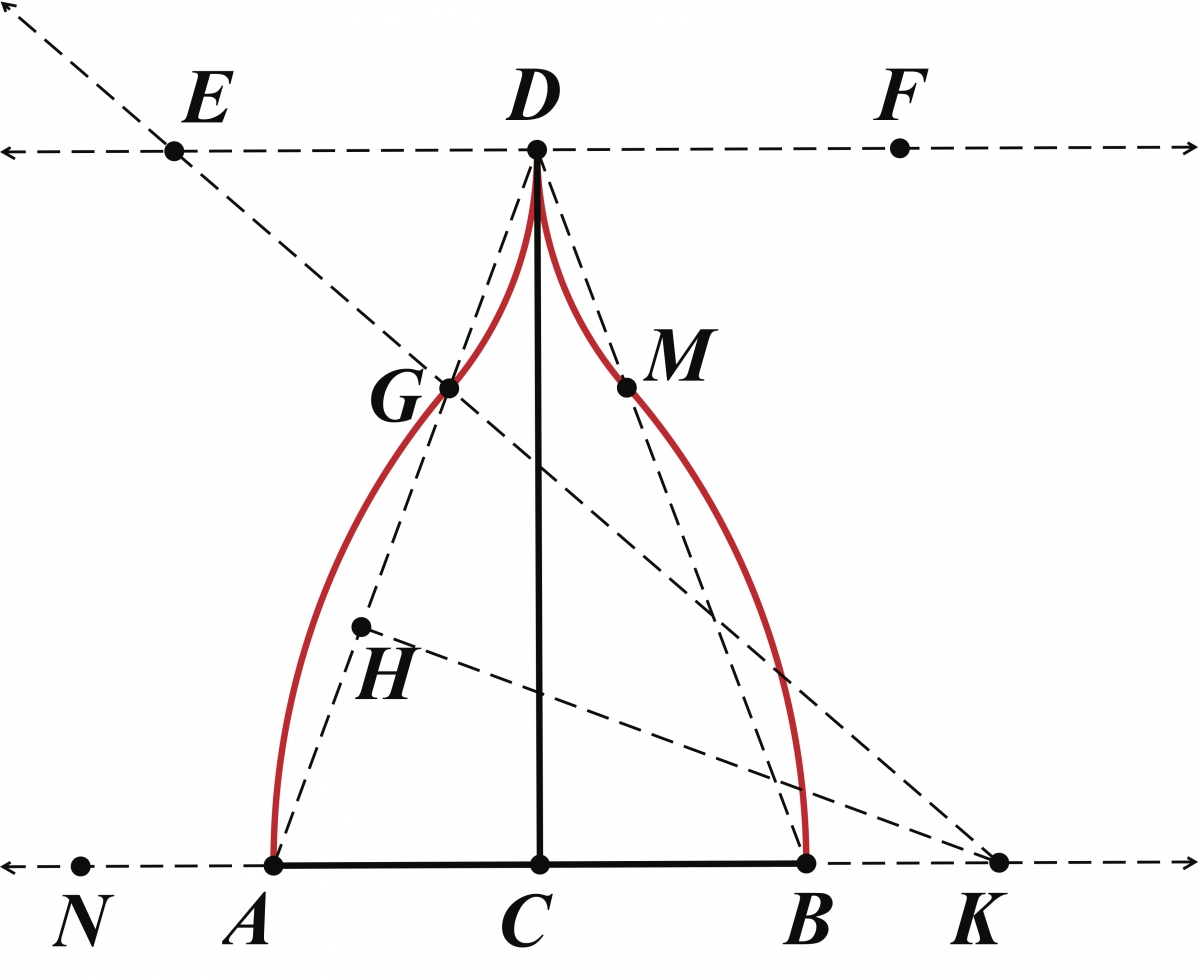
The construction she presented in the 1906 article is interesting in that, in addition to the traditional constructions of perpendicular and parallel lines, the infrequently encountered trisection of a segment of a given length is needed. Sykes’ directions are as follows with our comments added parenthetically in italics. The construction steps are illustrated in Figure 5.

• Given \(AB\) the span and \(CD\) the altitude. Draw the isosceles triangle \(\triangle ABD\).
• Divide \(AD\) into three equal parts. (That is, we have \(H\) and \(G\) on \(AD\) such that \(AH = HG = GD\).)
• Draw \(HK\) the perpendicular at the first point of division cutting \(AB\) at \(K\). (Thus, \(K\) lies on line \(AB\) and \(HK\) is perpendicular to \(AD\).)
• Draw \(KG\) (\(G\) the second point of division) cutting \(EF\) at \(E\). \(EF\) is parallel to \(AB\) through \(D\). (In other words, let \(E\) be the intersection of the line \(KG\) and the parallel to \(AB\) through \(D\). Construct \(F\) on this parallel so that \(ED = FD\).)

Figure 5: The Persian arch.

• \(K\) is center and \(KA\) radius and \(E\) center and \(ED\) radius for arcs \(AGD\). (Here we have two arcs of circles, one with center \(K\) and radius \(KA\), and the other with center \(D\) and radius \(ED\). These circles meet at \(G\) where, together, arcs \(\widehat{AG}\) and \(\widehat{GD}\) form the left half of the Persian arch.)
• On right side of figure \(FD\) equals \(DE\) and \(AN\) equals \(BK\) and the arcs drawn. (Thus, for the right half of the arch, we must construct \(N\) on \(AB\) such that \(NC = KC\). Then, we construct two circles, one with center \(N\) and radius \(NB\), and the other with center \(F\) and radius \(FD\).)

Sykes ended the construction by posing the following unanswered question: “Why do arcs meet at \(G\) and \(M\)?” To see why the circle with center \(K\) and radius \(KA\) passes through \(G\), one should note that \(H\)  is the perpendicular bisector of \(AG\), and thus, \(AK = GK\). Furthermore, the similarity of triangles \(\triangle EDG\) and \(\triangle KAG\) guarantees that \(ED = EG\).