Geometrical Representation of Arithmetic Series

Author(s):

Gautami Bhowmik (Université de Lille)

In the preceding case, \(a>\frac {d}{2}\) so the base is a positive number. In case \(a<\frac d {2}\) the sum of the series can still be represented as the signed area of a series figure. Note that \(a<\frac {d}{2}\) does not necessarily mean that any of the terms of the series are negative (for example, if \(a=2, d=5\)). In this case we get "negative areas" in the geometric representation until \(a-\frac {d}{2}+kd=0\) where \(k\) need not be an integer. Thus we may have two different areas corresponding to the negative and positive bases of the series-figure, i.e. for the two nearest integers \(k_1\) and \(k_2\) such that \(k_1\le k\le k_2.\)

\(S_n\)	\(= a+(a+d)+\cdots +(a+(n-1)d)\)
	\(=\left(a-\frac d{2}\right)+\frac d{2}+ \left(a+d-\frac d{2}\right)+\frac {d}{2}+\left(a+(n-1)d-\frac d{2}\right)+\frac d {2}\)
	\(={-\left[\left(\frac d{2}-a\right)-\frac d{2}+ \left(\frac d{2}-a-d\right)-\frac {d}{2}+\cdots +\left(\frac d {2}-a-k_1d\right) -\frac {d}{2}+\left(\frac d {2}-a-kd\right) \right]}\)
	\(\quad{\ +\left[\left(\frac d {2}-a-kd\right) +\left(a+k_2d-\frac{d}{2}\right)+\frac{d}{2}+\cdots +\left(a+(n-1)d-\frac d{2}\right) +\frac d {2}\right]}.\)

Since \(a+kd-\frac {d}{2}=0,\) the height of the negative triangle would be \(k=\frac{\frac {d}{2}-a}{d}\) while that of the upper triangle would be \(n-k.\)

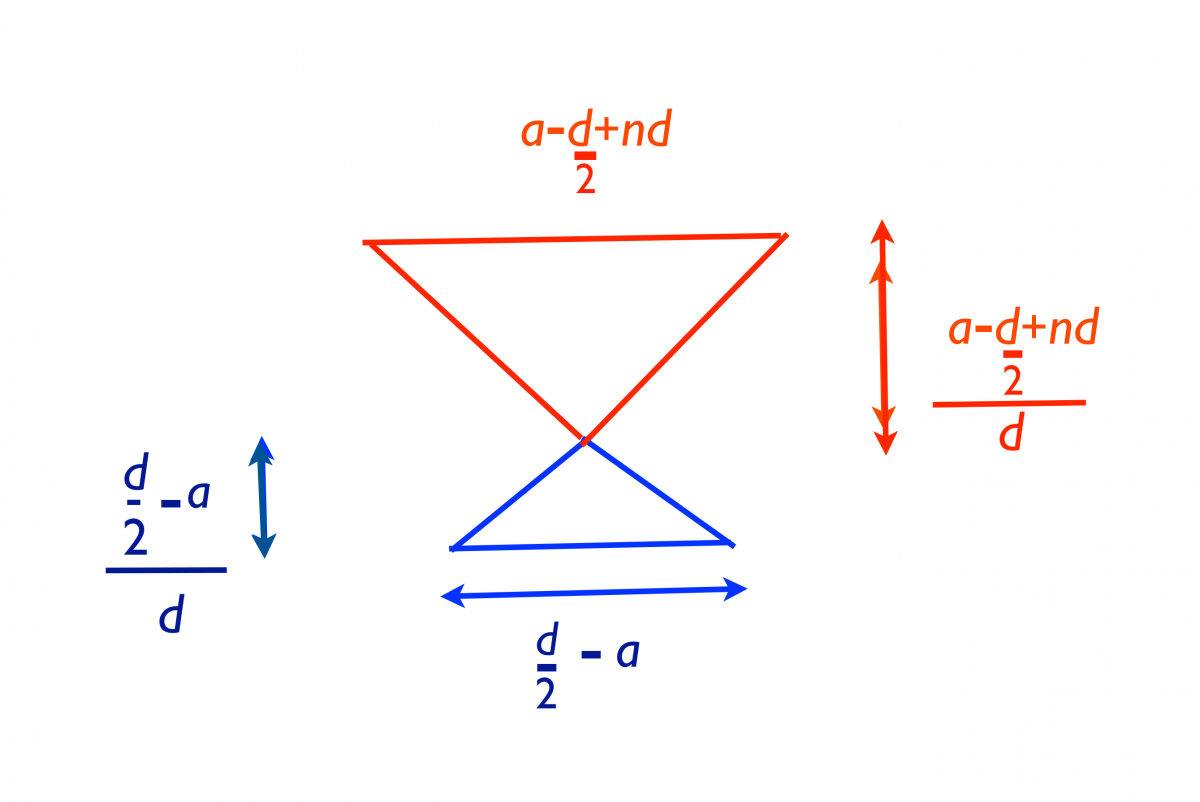
Figure 10. Series-figure with negative base

So in general when the base is negative and the face positive, the figure whose area we are interested in would be that in Figure 10, where the area of the triangle at the bottom is subtracted from that at the top.

This corresponds to what we find in a text, this time with ku for base, vivara for difference, and tryasra for triangle (Gaṇitakaumudī, vol. 2, pp. 86-87):

If the base is negative, however, the two sides will cross each other and grow. There will be two triangles, upper and lower, with the base and the face as the bases. The base and the face divided by the face minus the base and multiplied by the altitude are the altitudes of the two triangles. The difference of their areas is equal to the sum of the series.

For the heights of the lower and upper triangles denoted by \(h_1\) and \(h_2,\) respectively, we get

\(\frac{b}{f-b}n=\)	\(h_1=\frac{d/2-a}{nd}n\)
\(\frac{f}{f-b}=\)	\(h_2=\frac{a-d/2+nd}{nd}n\)

since \(f-b=\frac {d}{2}-a+nd-(\frac {d}{2}-a)=nd.\) Thus \(h_1\) obtained here is precisely the \(k\) that we had before.

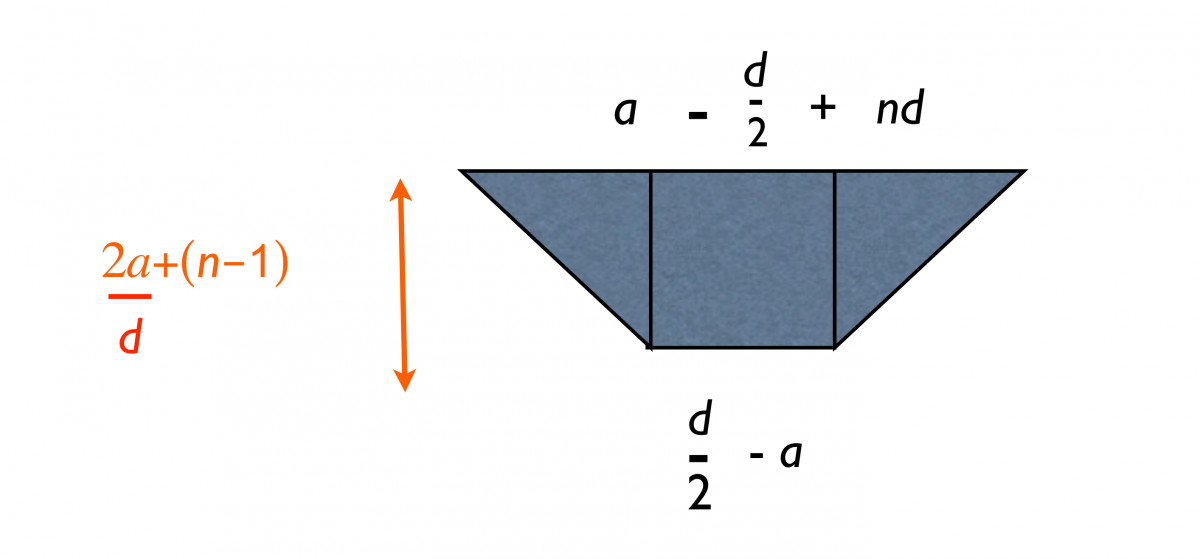
Figure 11. Triangles to trapezium

Notice that this again gives a trapezium with the same face and base, but the distance between the parallel lines is less than the height for the case where the base is positive. If both the base and face are negative the series-figure would be constructed exactly as for the case of positive base and face but the sum would be negative.

Gautami Bhowmik (Université de Lille), "Geometrical Representation of Arithmetic Series – The Twisted Trapezium," Convergence (December 2015)

Convergence

Tags:

History of Mathematics