Descartes’ Method for Constructing Roots of Polynomials with ‘Simple’ Curves - Sextic and Quintic Equations

Constructing the roots of sextic and quintic equations using a circle and a Cartesian parabola

At the end of his 'Geometry,' Descartes tackled an incredible problem: to somehow construct the roots to polynomial equations of degree 6. Aside from occurring in modern algebra classes, Descartes pointed out that solutions to sextic equations arise in the following geometry problems:

• certain 9-, 10-, 11-, 12-, and 13-line locus problems (Smith 25),
• finding four mean proportionals (Smith 236, 239),
• dividing an angle into five equal pieces (Smith 239), and
• inscribing a regular 11-gon or 13-gon in a circle (Smith 239).

Earlier in his 'Geometry,' Descartes explained that any polynomial equation can be converted to one that has all positive roots by replacing \(x\) by \(x\) minus a constant \(c\) larger than the absolute values of all of the polynomial's negative roots. This is because the roots of \(f(x-c)\) will each be greater than the roots of \(f(x)\) by the positive value \(c,\) making each of the roots of \(f(x-c)\) positive. Though Descartes did not explain exactly how to determine the size of this constant, he did give some guidance, writing (Smith 168):

This can be done even when the false [negative] roots are unknown, since approximate values can always be obtained for them and the roots can then be increased by a quantity as large as or larger than is required.

Descartes claimed further that, "When this is done, there will be no two consecutive \(+\) or \(-\) terms" (Smith 168), and that the coefficient of the third largest exponent could be made bigger than the square of half the coefficient of the second largest exponent (Smith 168, 220). (See Note on Descartes' 'Rule of Signs'.)

After these preliminaries, Descartes tackled the problem of constructing the roots to any sixth degree polynomial of the form \[x^{6}+px^{5}+qx^{4}+rx^{3}+sx^{2}+tx+u=0,\] where the coefficients \(p, r,\) and \(t\) are negative, the coefficients \(q,s,\) and \(u\) positive, and \(q>\left({\frac{p}{2}}\right)^2.\) Again, he claimed that sextic equations that do not meet these constraints can be transformed by a substitution of variables. He noted further that quintics could be solved by multiplying through by \(x\) and solving the resultant sextic (ignoring the solution \(x=0\)).

I will first describe Descartes’ solution process and analyze it afterwards.

The roots to the sextic equation of the form \[x^{6}+px^{5}+qx^{4}+rx^{3}+sx^{2}+tx+u=0\] can be constructed as follows:

Step 1. Construct the right branch of a Cartesian parabola with (positive) parameters \[n=\sqrt{q-\frac{t}{\sqrt{u}}-\frac{p^{2}}{4}},\quad{a=-\frac{2\sqrt{u}}{pn}},\quad{\rm{and}}\quad{b=-\frac{p}{2}}.\]

Figure 8. First step of Descartes' process for solving sextic equations. Instructions: Change the values of \(p, q, r, s, t,\) and \(u\) to see how the shape of the right branch of the Cartesian parabola changes. (The values shown for \(p,r,\) and \(t\) on the sliders are absolute values.) You may slide the vertex of the parabola up and down the \(y\)-axis, as well, to see how the line and parabola form the right branch of the Cartesian parabola. To hide the parabola and the line, uncheck the ‘hide/show sliding parabola’ checkbox.

Step 2. To find the real solutions to the sextic equation, place a point L at \((0,-a),\) so that L is \(a\) units below the origin B, and place a point H at \((0,k)\) where \(k=-\frac{t}{2n\sqrt{u}}-a.\) The length of line segment LH, then, is \(a+k.\) Extend a line segment horizontally from H into the first quadrant a distance \(h\) to point I, where \[h=-\frac{r}{2n^{2}}+\frac{\sqrt{u}}{n^{2}}+\frac{pt}{4n^{2}\sqrt{u}}.\] Construct a circle with LI as its diameter. Construct another circle with center L and radius \(\sqrt{\frac{s-p\sqrt{u}}{n^{2}}}\) and call one (or both) of the intersection points of the two circles P.

Figure 9. Second step of Descartes' process for solving sextic equations. Instructions: Change the values of the coefficients \(p, q, r, s, t,\) and \(u\) to see how the Cartesian parabola, the circles, and the triangle change.

Step 3. Finally, construct a circle with center I which passes through point P. Then the \(x\)-coordinates of the intersections of that circle with the Cartesian parabola are the roots of the original equation.

Figure 10. Third step of Descartes' process for solving sextic equations. Instructions: Change the values of \(p, q, r, s, t,\) and \(u\) to see how the intersections with the circle change to give the real solutions to the sextic equation. By adjusting the values of the coefficients, you can obtain examples of degree 6 polynomials having four, two, and no positive real roots, along with, respectively, two, four, and six imaginary roots. This leaves one case, that of six positive real roots.

Here is the actual diagram from the 'Geometria,' in which Descartes' axes are oriented in the opposite direction of how we orient them today. Point B is the origin, point D is the vertex of the sliding parabola, point A is the fixed point of the intersecting line segment, point C is a point on the Cartesian parabola, and point I is the center of the circle.

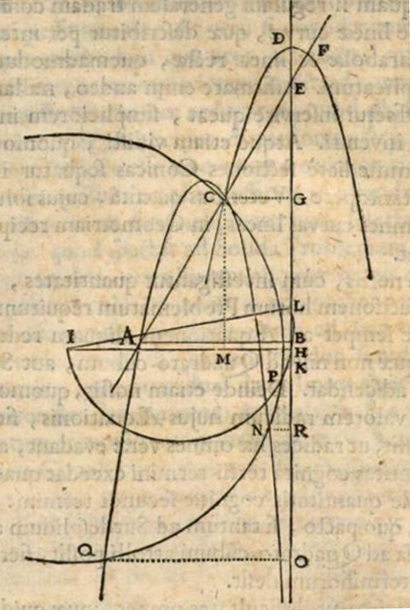
Figure 11. Descartes' method for finding solutions for degree 6 polynomials. The diagram above appears in Frans van Schooten's translation of Descartes' French ‘La Géométrie’ into the Latin 'Geometria.' Van Schooten's first edition appeared in 1649; this image is from his 1659 second edition, available via Google Books. The original diagram appeared in Descartes' 1637 ‘La Géométrie’ on page 404 of his longer Discours de la Methode and on page 222 of Smith's and Latham's facsimile (and English translation) of ‘La Géométrie.’

Descartes merely stated his process and, for his ‘proof,’ showed that by starting with \(b, n, a, h, k,\) and radius IP in terms of \(p, q, r, s, t,\) and \(u,\) the intersections would correspond to roots of the sextic equation \[x^{6}+px^{5}+qx^{4}+rx^{3}+sx^{2}+tx+u=0.\] It will be shown later in this article how to derive \(b, n, a, h, k,\) and radius IP from the coefficients \(p, q, r, s, t,\) and \(u\) of the polynomial. First, we'll consider an example of a sixth degree polynomial with six positive real roots.

Note on Descartes' 'Rule of Signs'

If all of the roots of a polynomial are real, Descartes' own "rule of signs" guarantees that the coefficients of the polynomial must alternate between \(+\) and \(-\) in order for all of its roots to be positive. In this case, if the polynomial does have some negative roots, the signs will not alternate throughout, but if the function \(f(x-c)\) for big enough \(c\) is created then the signs of the coefficients of the new polynomial will alternate and its roots will all be positive.

Descartes stated his famous "rule of signs" a few pages before the discussion cited above (Smith 160):

An equation can have as many true [positive] roots as it contains changes of sign, from \(+\) to \(-\) or from \(-\) to \(+\); and as many false roots as the number of times two \(+\) signs or two \(-\) signs are found in succession.

This statement allows for the possibility of complex roots, and Descartes applied his strategy described above for making all negative roots positive to polynomials with both real and complex roots. One way to be certain all real roots are positive is to make sure the signs of the coefficients of the polynomial alternate between \(+\) and \(-\) throughout. However, a sixth degree polynomial, for instance, can have 0, 2, 4, or 6 complex roots (since complex roots occur in pairs) and 6, 4, 2, or 0 positive real roots, respectively. In all four cases, all of the real roots are positive, but, according to Descartes' "rule of signs," only the case of six positive real roots requires six sign changes. We consider the special case of a sixth degree polynomial with six positive real roots on the next webpage.

Return to general process for sixth degree polynomials.