- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Cubes, Conic Sections, and Crockett Johnson - Conic Sections and Doubling a Cube
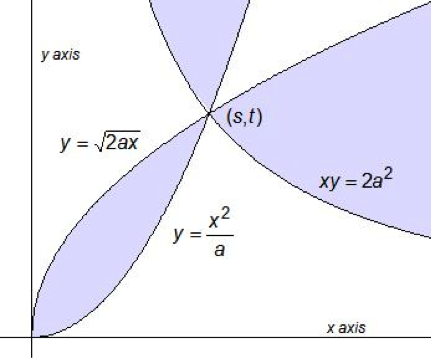
Figure 7. Two parabolas meeting a hyperbola at the point \((s,t).\) (Constructed using Geometer’s Sketchpad.)
Given a cube with edge of length \(a,\) how do we now utilize conic sections to double that cube; i.e., how do we find \(x\) so that \(x^3=2a^3\)? Consider the point of intersection, \((s,t),\) in Figure 7 above. The curves in this figure represent the parabolas \(x^2=ay\) and \(y^2=2ax,\) together with the hyperbola \(xy=2a^2;\) i.e., the graphs of the functions \[y={\frac{x^2}{a}}, {y=\sqrt{2ax}},\,\,{\rm{and}}\,\,{y={\frac{2a^2}{x}}},\] for \(x>0.\) The equation of the first function tells us that \(t={{s^2}/{a}},\) so that the equation of the second parabola becomes \[{\left({\frac{s^2}{a}}\right)}^2={2as},\,\,{\rm or}\,\,\,s^3=2a^3.\] Thus the \(x\)-coordinate of the point of intersection, \(s,\) is the length of the edge of a cube which is double the volume of the original cube with edge of length \(a.\) If we look at the cube of the \(y\)-coordinate of the point we find \[t^3={\frac{s^6}{a^3}}={\frac{(s^3)^2}{a^3}}={\frac{4a^6}{ a^3}}=4a^3\] so the \(y\)-coordinate is the length of the edge of a cube which is quadruple the volume of the original cube, or the larger of the mean proportionals mentioned previously.
Stephanie Cawthorne (Trevecca Nazarene University) and Judy Green (Marymount University), "Cubes, Conic Sections, and Crockett Johnson - Conic Sections and Doubling a Cube," Convergence (March 2014)




