A Translation of Evangelista Torricelli's Quadratura Parabolae - Torricelli's Quadrature of the Parabola (One Version)

Torricelli's Quadrature of the Parabola (One Version)

The method of exhaustion was a logically sound approach to solving area and volume problems. However, as Boyer notes, "the cumbersomeness of its application led later mathematicians to seek a more direct approach to problems in which the application of some such procedure would have been indicated" [Boyer, p. 35]. In the seventeenth century, Cavalieri's method was the premier example of this "more direct approach", and in the section of de Dimensione Parabolae, given in translation below, Torricelli presented eleven different examples of how to find the quadrature of the parabola using Cavalieri's method and other infinitesimal methods. Modern interpretations of some of these Cavalierian approaches have already been given in [Anderson, p. 356] and [Leahy, pp.178-183]. As a specific example we will discuss another approach found in Proposition 15 of the work. (See also [Baron, p. 183-185] for another discussion of this result.)

What was noteworthy about the approach in Proposition 15 was that it directly extended Archimedes' own technique for finding the quadrature of the parabola. More precisely, whereas Archimedes stopped after finitely many terms of his geometric series and let the method of exhaustion take care of the rest, Torricelli used a geometrical argument to demonstrate how to add the infinitely many terms of the same geometric series and arrive at the same area formula.

To justify this infinite summation Torricelli introduced a geometrical figure he called a flexilineum, which was constructed as follows: Consider two lines $B_1D$ and $C_1D$ that intersect at $D$, and a sequence of points $B_1,B_2,\dots$ on $B_1D$, and $C_1,C_2,\dots$ on $C_1D$ such that for $i=1,2,\dots$ the segments $B_iC_i$ are mutually parallel, as are the segments $B_{i+1}C_i$. The flexilineum consisted of the infinitely many conjoined segments $B_1C_1B_2C_2\dots$.

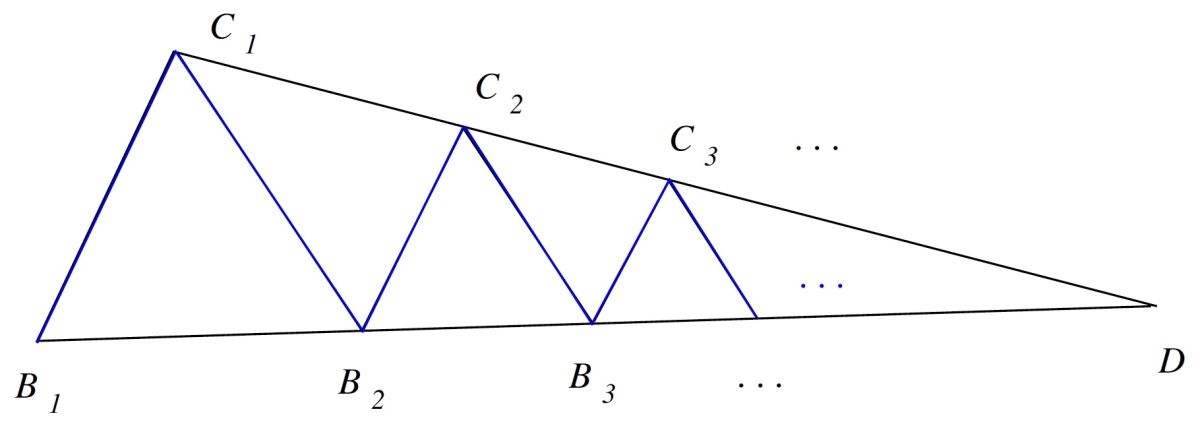
Torricelli made several observations about the flexilineum that were key to his proof. First, he noted that the terms of the sequence of lengths $B_iC_i$ are in a continuous geometric proportion. That is, $$\frac{B_1C_1}{B_2C_2}=\frac{B_2C_2}{B_3C_3}=\frac{B_3C_3}{B_4C_4}=\cdots.$$ To see why, note that since both families of line segments $B_iC_i$ and $B_{i+1}C_i$ are parallel among themselves, Euclid VI.2 implies that for each $i$, $\triangle B_iC_iD$ is similar to $\triangle B_{i+1}C_{i+1}D$, and $\triangle B_{i+1}C_iD$ is similar to $\triangle B_{i+2}C_{i+1}D$. So by similar triangles we have $$\begin{eqnarray*} \frac{B_iC_i}{B_{i+1}C_{i+1}} &= \frac{C_iD}{C_{i+1}D} \\ &= \frac{B_{i+1}D}{B_{i+2}D} \\ &= \frac{B_{i+1}C_{i+1}}{B_{i+2}C_{i+2}}, \end{eqnarray*}$$ and the result follows. A similar argument shows that the line segments $B_{i+1}C_i$ are also in a continuous geometric proportion.

Torricelli's second and most important result about the flexilineum was the derivation of a geometrical representation for the sum of the lengths of the infinitely many line segments $B_iC_i$. To find this sum geometrically, he extended each of the segments $B_{i+1}C_i$ so that they intersected the extension of $B_1C_1$ in a point we will call $D_{i+1}$. (Note: $D_1=B_1$ and $D_2=C_1$ by definition as well.) Similarly, he let the line parallel to all the $B_{i+1}C_i$ and passing through $D$ intersect the extension in a point $L$.

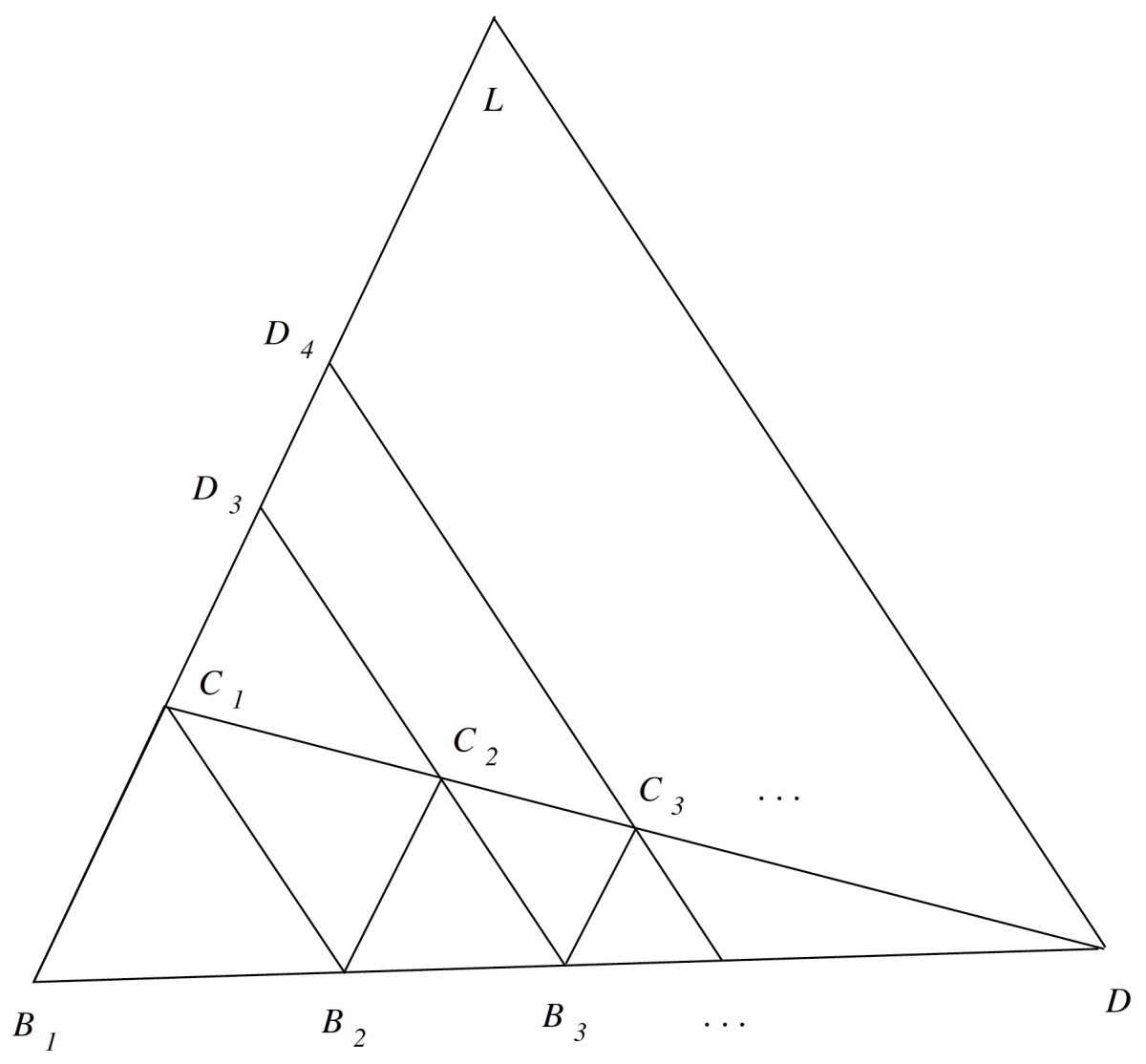
All of the lines $B_iD_i$ are parallel to each other. By assumption, the lines $B_iC_i$ are parallel to each other as well. Consequently the quadrilateral $D_iB_iC_1D_{i+1}$ is a parallelogram, so $D_iD_{i+1}=B_iC_i$ and the length of the segment $B_1L$ (that is, the infinite sum of the lengths of all of the $D_iD_{i+1}$ segments) is clearly the same as the infinite sum of the lengths of all of the segments $B_iC_i$.

Torricelli was so concerned to get this proof right that he spent several pages filling in details. He noted, for instance, that even though the proof deals with ratios of lengths, it is still valid for ratios of any other type of magnitude [Torricelli, p. 67]. It's also an easy exercise to show that given any ratio $a/b$, it's possible to construct a flexilineum such that $B_iC_i/B_{i+1}C_{i+1}=a/b$.

Returning to the original problem of the quadrature of the parabola, let $B_iC_i$ represent $A_i$, the area of the triangles added at the $i$${}^{}$ stage of Archimedes' construction. Then by Archimedes' construction the segments $B_iC_i$, $i=1,2,\dots$, are in a continuous geometrical proportion in a ratio of 1 to 4. That is, $$\frac{1}{4}=\frac{B_1C_1}{B_2C_2}=\frac{B_2C_2}{B_3C_3}=\cdots.$$ With this interpretation, Torricelli's flexilineum showed that the sum of the areas $A_1,A_2,\dots$ (i.e., the area of the segment of the parabola) is the same as the length $B_1L$.

The final step in Torricelli's proof was to compute $B_1L$. To find the length of $B_1L$, he established a proportion amongst

1. the first length $B_1C_1$ (which is the area of the first triangle $\triangle QPq$ in Archimedes' construction),
2. the extended length $B_1L$ (which is the area of the segment $Parab(QPq)$ of the parabola), and
3. the difference  $B_1C_1-B_2C_2$ (which is the difference between the first triangle and the triangles added at the second step--that is, $\frac{3}{4}\triangle PQq$).

To see this proportional relation, note that if $V$ is placed on $B_1L$ so that $VB_2$ is parallel to $C_1D$, then $VC_1=B_2C_2$, since $VC_1C_2B_2$ is a parallelogram.

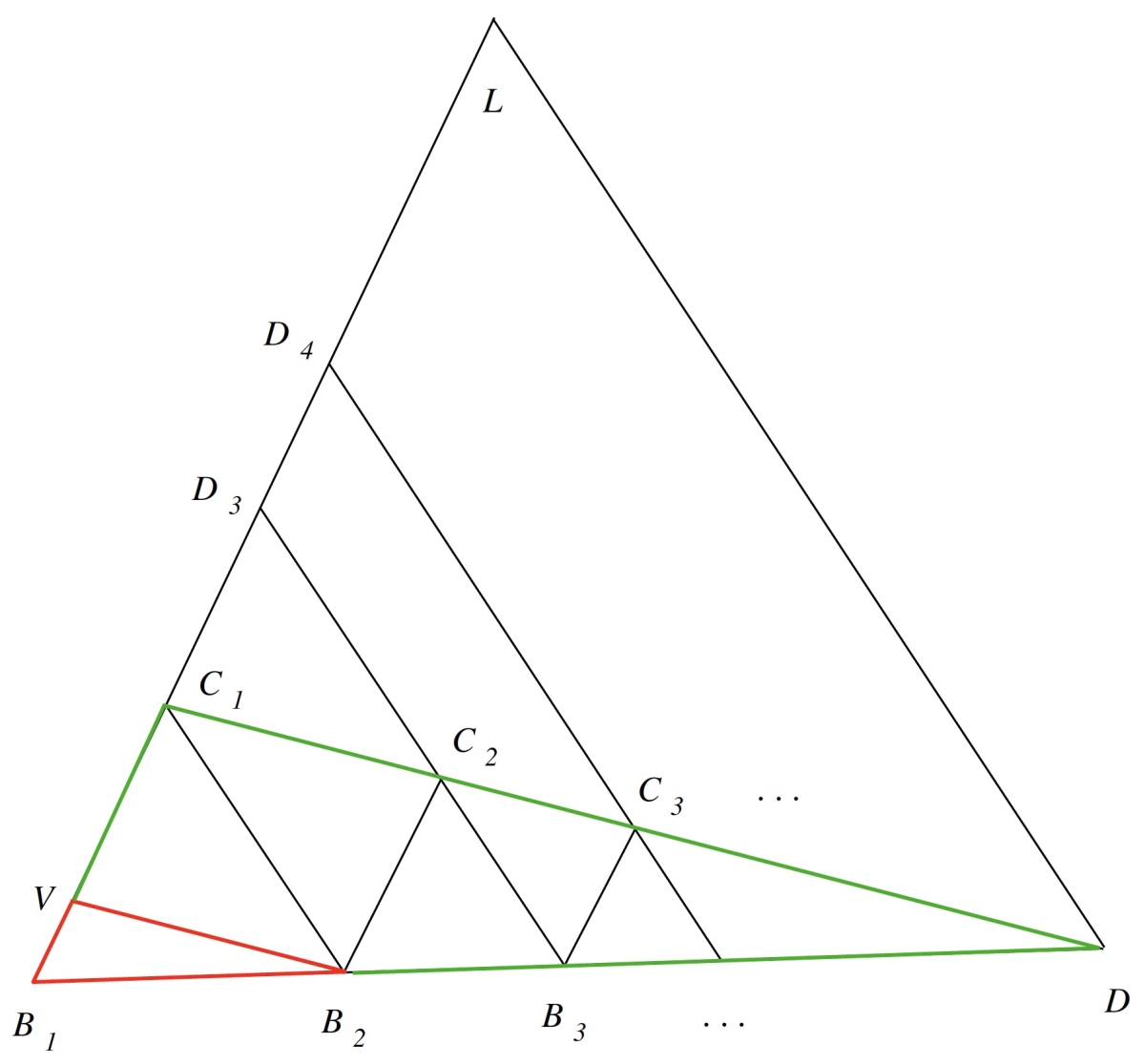
Likewise, we have $\triangle B_1VB_2$ similar to $\triangle B_1C_1D$ and $\triangle B_1C_1B_2$ similar to $\triangle B_1LD$. With some work, the similarity of these triangles can be used to show: $$\frac{B_1C_1-B_2C_2}{B_1C_1}=\frac{B_1V}{B_1C_1}=\frac{B_1B_2}{B_1D}=\frac{B_1C_1}{B_1L},$$ which we can solve for $$B_1L=\frac{(B_1C_1)^2}{(B_1C_1-B_2C_2)}.$$ In terms of the quadrature of the parabola, this means $$Parab(PQq)=\frac{(\triangle PQq)^2}{\frac{3}{4}\triangle PQq}=\frac{4}{3}\triangle PQq,$$ and thus Torricelli derived Archimedes' quadrature formula for a segment of a parabola.