A Translation of Evangelista Torricelli's Quadratura Parabolae - Archimedes' Quadrature of the Parabola

Archimedes' Quadrature of the Parabola

Torricelli's de Dimensione establishes the amazing result that Archimedes' computation of the area of a segment of a parabola is logically equivalent to most of the major geometrical results known at the time. Given its centrality to Torricelli's work, it's useful to review in modern terms the key result in Archimedes' Quadrature of the Parabola, which determines the area of a segment of a parabola in terms of an inscribed triangle:

Proposition 24 of QP: Every segment bounded by a parabola and a chord $Qq$ is equal to four-thirds of the triangle which has the same base as the segment and equal height [Heath, p. 251].

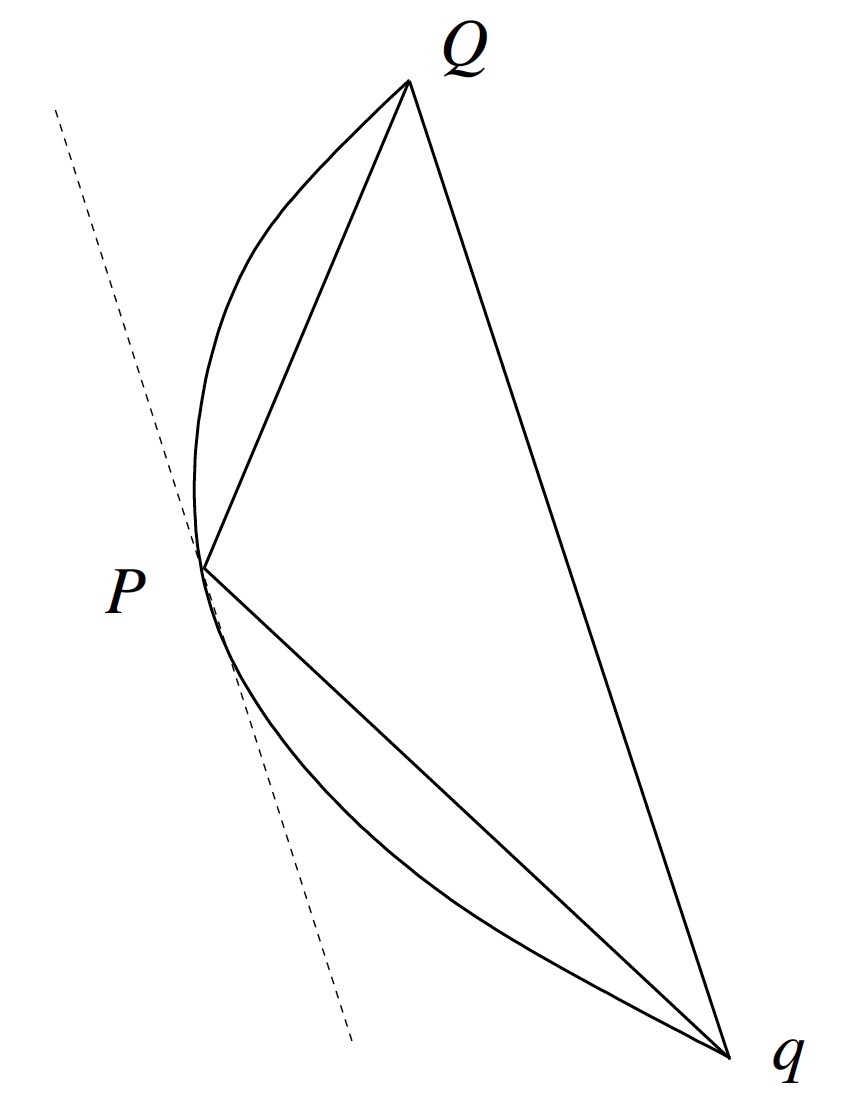
Archimedes' proof of this result (see also, e.g., [Katz, pp. 108-109] or [Boyer, pp. 52-53]) is an application of the method of exhaustion, which was the traditional approach among Greek mathematicians for solving area and volume problems. The proof also hinges on what is essentially a summation formula for a finite geometric series and an ingenious observation about how triangles can be inscribed inside a segment of a parabola. This result about inscribed triangles in turn depends on two more fundamental properties about the nature of the parabola which can be found in [Heath, p. 248]:

1. Given any chord $Qq$ in a parabola and the point $P$ on the parabola where the tangent at $P$ is parallel to $Qq$, the line $PV$ parallel to the axis of the parabola bisects $Qq$.

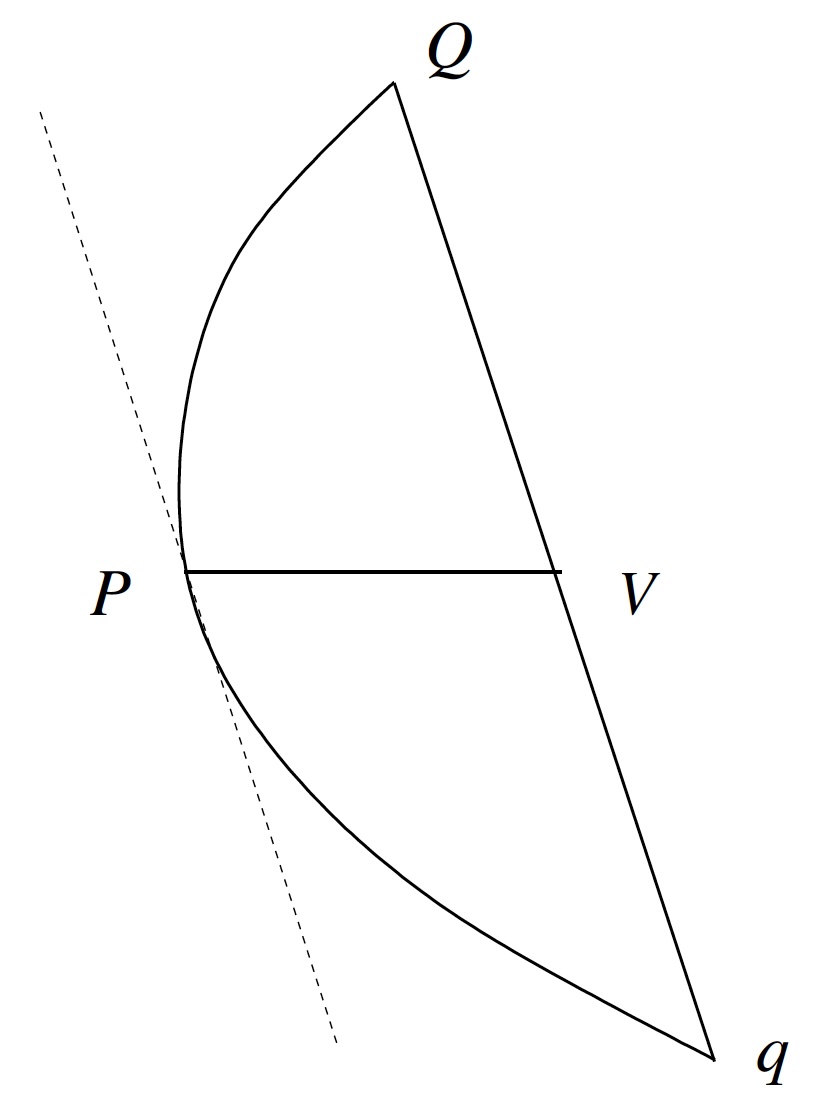
2. Given $Qq$ and $PV$ as above, if the points $W$ on $PV$ and $R$ on the parabola are such that $RW$ is parallel to $Qq$, then $$\frac{PV}{PW}=\frac{QV^2}{RW^2}.$$

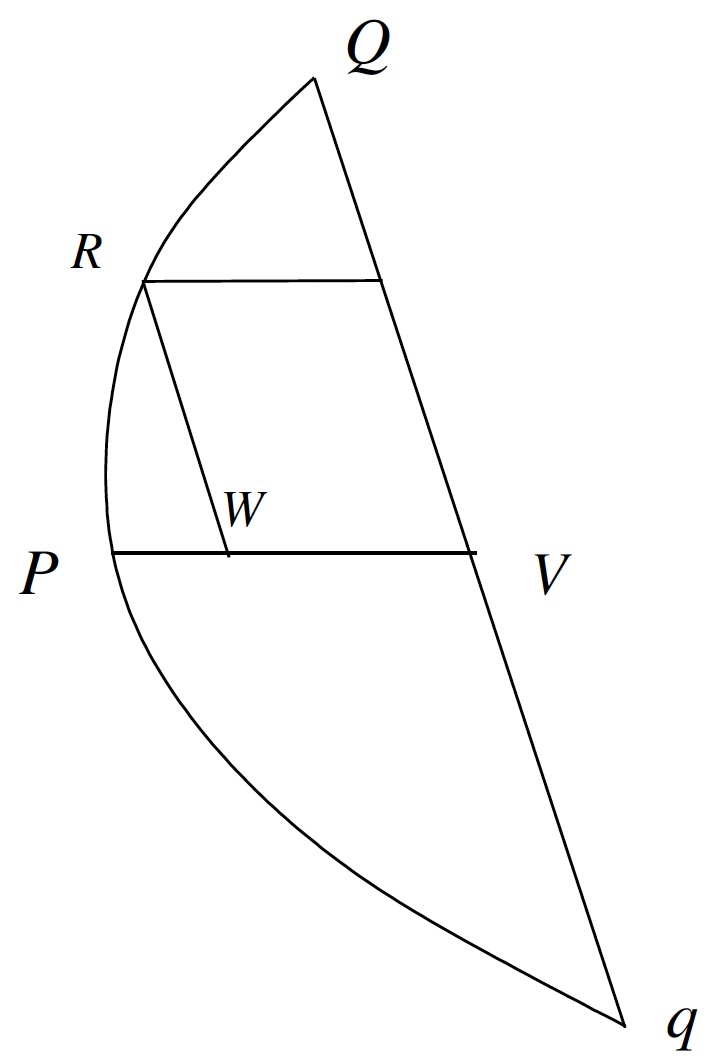
With these results in hand, Archimedes constructs a sequence of successively smaller and non-overlapping triangles inscribed inside of the segment of the parabola. Starting with the original triangle $\triangle PQq$ from the proposition, another triangle $\triangle PRQ$ with one-eighth the size of $\triangle PQq$ and inscribed in the parabola along the side of $PQ$ of $\triangle PQq$ is constructed as follows: With $Qq$ bisected at $V$, consider the point $M$ bisecting $QV$ and the point $R$ on the parabola such that $RM$ is parallel to $PV$ (and hence parallel to the axis of the parabola itself by definition of $PV$). Label the intersection of $RM$ and $PQ$ by $Y$ and let $RW$ be parallel to $Qq$.

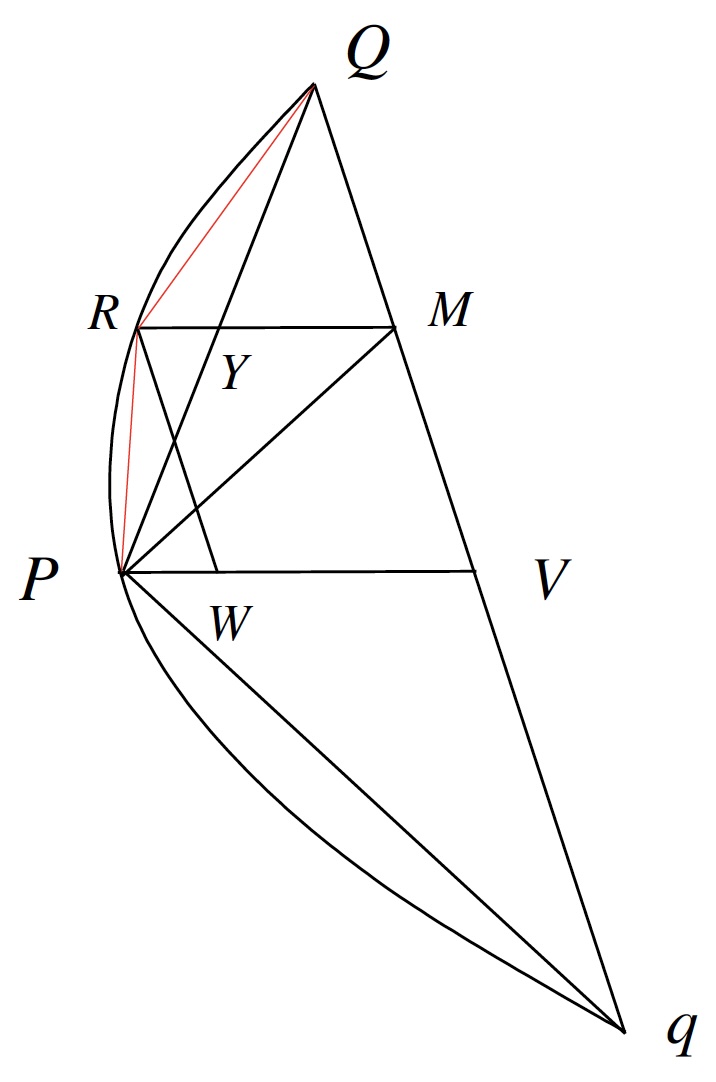
It follows that $RM$ is 3/4 of $PV$. Why? From property (2) above, $$\frac{PV}{PW}=\frac{QV^2}{RW^2}=\frac{(2MV)^2}{RW^2}=4\cdot\frac{RW^2}{RW^2}=4,$$ because $RMVW$ is a parallelogram (and thus $MW=RV$). This implies that $\frac{1}{4}PV=PW$ and so $RM=WV=PV-PW=\frac{3}{4}PV$. Now note that the triangles $\triangle QYM$ and $\triangle QPV$ are similar because $RM$ and $PV$ are parallel. Since $QM=\frac{1}{2}QV$, this similarity implies that $YM=\frac{1}{2}PV$ as well. Hence $YR=RM-YM=\frac{1}{4}PV$ and so $YM=2YR$. Thus, $\triangle PRQ$ and $\triangle PMQ$ have the same base ($PQ$), but the height of $\triangle PMQ$ is twice the height of $\triangle PRQ$, and it follows that in terms of area $\triangle PMQ=2\triangle PRQ$.

Likewise, $\triangle PQM$ and $\triangle PQV$ have the same height but $\triangle PQV$ has twice the base of $\triangle PQM$, so we also have $\triangle PQV=2\triangle PQM$ in terms of area. A similar argument shows that $\triangle PQq=2\triangle PQV$. It follows that  $\triangle PRQ=\frac{1}{8}\triangle QPq$, because $8\triangle PRQ=4\triangle QPM=2\triangle PQV=\triangle QPq$. A triangle $\triangle Pqr$ with the same ratio to  $\triangle PQq$ can likewise be constructed on the side$Pq$, so altogether the original triangle has four times the total area of the two newly-constructed triangles.

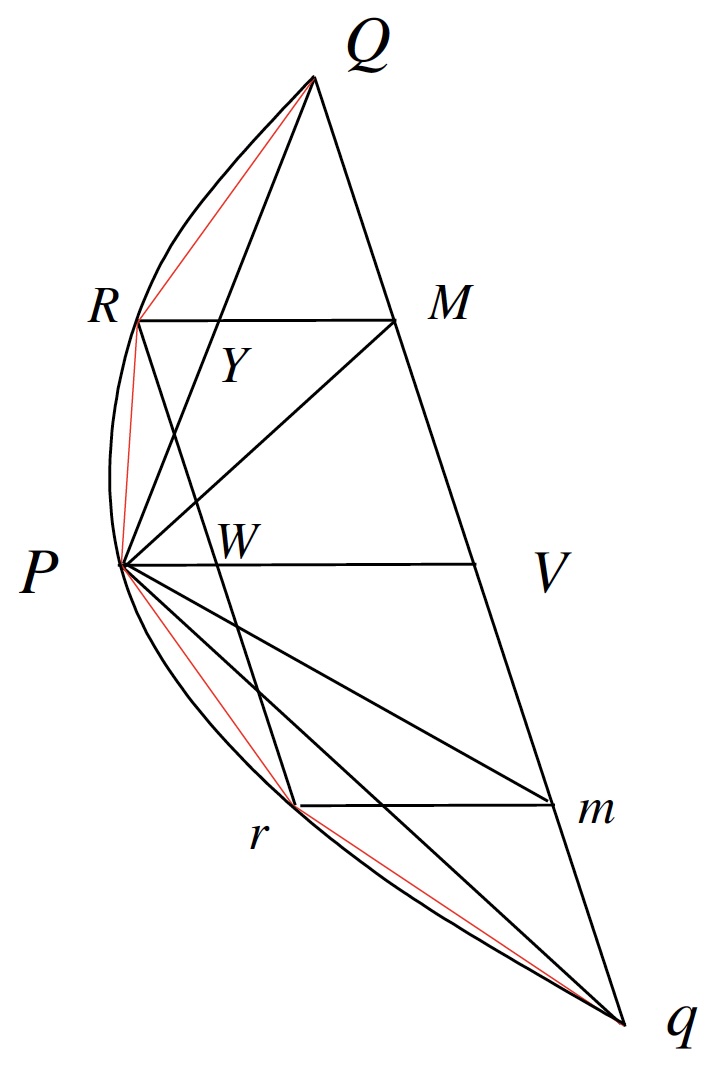
Also, note the geometrically obvious fact that the area of the three triangles together make an even better approximation to the area of the segment of the parabola (which we will denote by $Parab(PQq)$ in what follows) than the first triangle alone.

But why stop there? Each line $PQ$ and $Pq$ is itself the base of a segment of the parabola and $rm$ and $RM$ are parallel to the axis of the parabola (just like $PV$), so the same construction can be applied to the sides of $\triangle PQR$ and $\triangle Pqr$, resulting in four new triangles with combined area $\left(\frac{1}{4}\right)^2\triangle PQq$. Obviously, the sum of these seven triangular areas is an even better approximation to the area of the segment of the parabola. And so on. As Archimedes will show eventually (see the discussion of the method of exhaustion below), the difference between the sums of these triangular areas and the area of the sector of the parabola is going to zero as $n$ gets larger. At the $n$th step of the approximation another $\left(\frac{1}{4}\right)^n\triangle PQq$ is added to the approximation, so the total area of the approximation after $n$ stages is the finite geometric series  $$\triangle PQq + \frac{1}{4}\triangle PQq + \left(\frac{1}{4}\right)^2\triangle PQq +\cdots+ \left(\frac{1}{4}\right)^n\triangle PQq.$$

The next observation in Archimedes' proof is essentially (from our perspective today) an algebraic identity that was designed to understand how this finite geometric series determined by the triangular areas grows as more triangles are added. Note first that for any quantity $A$, simple arithmetic shows that $$\frac{1}{4}A+\frac{1}{3}\cdot\frac{1}{4}A=\frac{1}{4}A+\frac{1}{12}A=\frac{1}{3}A.$$ Next, consider a finite sequence $A-1,A_2,\dots,A_n$ such that $A_i=\frac{1}{4}A_{i-1}$. Since $\frac{1}{4}A_i+\frac{1}{12}A_i=\frac{1}{3}A_i$ for each $i$, $$\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{12}A_1+\cdots+\frac{1}{12}A_n=\frac{1}{3}A_1+\cdots+\frac{1}{3}A_n.$$ But since $4A_i=A_{i-1}$, for $i=2,3,\dots,n$, we have $\frac{1}{12}A_{i-1}=\frac{1}{3}A_i$, and this equation can be rewritten as $$\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_2+\cdot+\frac{1}{3}A_{n+1}=\frac{1}{3}A_1+\cdots+\frac{1}{3}A_n.$$ By canceling, this becomes  $$\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1}=\frac{1}{3}A_1.$$ Adding $A_1$ to both sides, we have Archimedes' geometric summation formula: $$A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1}=\frac{4}{3}A_1.$$

If $A_1=area(\triangle PQq)$, then $(1/4)A_1$ is the area of the triangles added at the second step, $(1/4)A_2$ is the area of the triangles added at the third step, and so on. So from a modern perspective, the identity  $$A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1}=\frac{4}{3}A_1$$ makes Archimedes' area formula geometrically obvious. The right-hand side never changes as $n\rightarrow\infty$. On the left-hand side, since $A_{n+1}=(1/4)^n\triangle PQq$, $\frac{1}{3}A_{n+1}\rightarrow 0$ as $n\rightarrow\infty$. The remaining terms are the sum of the inscribed, non-overlapping triangular areas, which converge to the area of the parabola. Thus, Archimedes' area formula, $Parab(PQq)=\frac{4}{3}\triangle PQq$, follows.

However, Archimedes would never take that step. Greek mathematicians, perhaps stung by the criticisms of Zeno of Elea (490-430BCE) in his paradoxes (or perhaps not--see [Baron, p. 22-25]), did not use infinite processes in formal proofs and never developed the concept of the limit. Instead, Archimedes employed the method of exhaustion, a technique found first in Antiphon, later perfected by Eudoxus, and adopted by Archimedes and others [Boyer, p. 32]. This was the standard method of solving area and volume problems for Greek mathematicians and, unlike our modern approach, doesn't require passage to the limit at any step. But it pays for this conceptual clarity with a lengthy double reductio ad absurdum proof, and that's exactly the sort of proof that Archimedes submits in the Quadrature of the Parabola.

In particular, to show that the area equation $Parab(QPq)=\frac{4}{3}\triangle QPq$ is true, Archimedes supposes that the equation isn't true. Then there are two possible relations between the areas:

1. $Parab(QPq)>\frac{4}{3}\triangle QPq$
2. $Parab(QPq)<\frac{4}{3}\triangle QPq$.

Both of these will be shown to lead to a contradiction.

To show that $Parab(QPq)>\frac{4}{3}\triangle QPq$ yields a contradiction, Archimedes notes that since each inscribed triangle is greater than half of the parabolic segment in which it lies (see [Heath, p. 248]), the sum of the triangular areas $A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n$ can be made as close to $Parab(QPq)$ as we want for large enough $n$. In particular, since $\frac{4}{3}\triangle QPq<Parab(PQq)$ by assumption, we must also have $$\frac{4}{3}\triangle QPq<A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n$$ for some finite number $n$. However, $$A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n<A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1},$$ and his algebraic identity for the geometrical series shows:  $$A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1}=\frac{4}{3}A_1=\frac{4}{3}\triangle PQq,$$ and so $\frac{4}{3}\triangle QPq<\frac{4}{3}\triangle QPq$. Hence a contradiction.

To show that $Parab(QPq)<\frac{4}{3}\triangle QPq$ yields a contradiction, note that since $A_{n+1}=\left(\frac{1}{4}\right)^nA_1$, it follows that $A_{n+1}$ can be made arbitrarily small for some finite $n$. Since (by assumption) $Parab(QPq)<\frac{4}{3}A_1$, we have  $$A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n+\frac{1}{3}A_{n+1}=\frac{4}{3}A_1>Parab(QPq).$$ Because $A_{n+1}$ can be made arbitrarily small, this shows we must eventually have $A_1+\frac{1}{4}A_1+\cdots+\frac{1}{4}A_n>Parab(QPq)$ for some finite $n$. Hence another contradiction--this time of the fact that each of the non-overlapping regions $A-1,A_2,\dots,A_n$ is inscribed in the segment of the parabola $Parab(QPq)$, so their sum must be smaller than the area of $Parab(QPq)$.

By trichotomy, $Parab(QPq)=\frac{4}{3}\triangle QPq$is the only possibility.