- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Translation of Evangelista Torricelli's Quadratura Parabolae - Some Historical Background
Some Historical Background
It's impossible to talk about Torricelli without introducing some other figures who were undoubtedly his most important mathematical influences: Galileo Galilei, Bonaventura Cavalieri, and the relatively unknown figure of Benedetto Castelli. Galileo (1563-1642) was, of course, the famous Italian scientist whose trouble with the Roman Inquisition is discussed even to this day. Cavalieri (1598-1647) was the 17th century mathematician whose work formalizing indivisibles would be the basis for Torricelli's work in de Dimensione Parabolae. However, it was Castelli (1578-1643) who would undoubtedly have the most important social and mathematical impact on Torricelli's life.

Benedetto Castelli.
Wikimedia Commons.
Born Antonio Castelli to relatively wealthy parents in Brescia, Castelli took the name Benedetto when he entered the Benedictine monastic order in 1595. Eventually, he was transferred to a monastery in Padua, where Galileo had been teaching since 1592. Castelli became Galileo's student, and eventually the two became close friends, as evidenced by their frequent correspondence after Castelli was transferred to another monastery near Naples in 1607. In 1610, when the publication of Sidereus Nuncius enabled Galileo to obtain a position as Chief Mathematician to the Medicis with a nominal position in mathematics at the University of Pisa, Castelli quickly obtained a transfer to a Benedictine Abbey in Florence. In 1613, with Galileo's help, Castelli too obtained a professorship in mathematics at the University of Pisa, where he remained until 1626, when he took a position teaching mathematics and solving problems in hydraulics for the Pope in Rome. Significantly, there was no Benedictine monastery in Pisa, so Castelli resided in a Jesuati monastery which from 1616 to 1620 was also the home of a young Jesuati named Bonaventura Cavalieri. Castelli was widely regarded as an outstanding teacher, and it was from Castelli that Cavalieri learned much of his mathematics. Castelli also introduced Cavalieri to Galileo, with whom Cavalieri exchanged more than 100 letters.
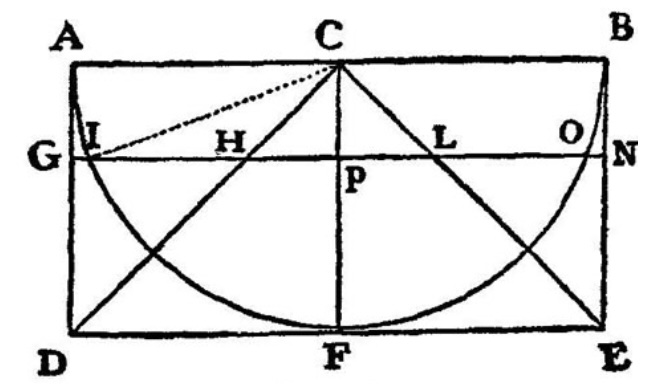
One of the interests these men shared was a mathematical technique called the method of indivisibles, which determined ratios between plane or solid figures by dividing them up into parallel, indivisible slices and studying the ratios of these slices. They weren't the first to stumble on this approach. (Unbeknownst to seventeenth century mathematicians, Archimedes had discovered a similar technique in his lost work on The Method of Mechanical Theorems. Johannes Kepler (1571-1630), who discovered the laws of planetary motion and was a Galileo correspondent, had also utilized similar ideas in his Nova stereometria doliorium vinariorum.) But they were probably the ones most responsible for promoting it. In his Dialogues Concerning Two New Sciences (1638) Galileo demonstrated the equality between the volume of a "soup bowl" AFBED of revolution to a cone DCE of the same height by demonstrating that on each planar slice perpendicular to the shared axis CF of the figures, the annulus on ON had the same area as the circle on radius PL. (See [Baron, p. 119] and [Katz, p. 515].)
Cavalieri's Geometria indivisibilibus continuorum nova quadam ratione promota was intended to be the most thorough exposition of the theory of indivisibles that was available at the time. However, as Andersen notes, it was "so difficult that [nineteenth century mathematical historian] Maximilien Marie suggested that if a prize existed for the most unreadable book, it should be awarded to Cavalieri for Geometria" [Andersen, p. 294].

Evangelista Torricelli.
Wikimedia Commons.
Torricelli was a latecomer to this group of mathematicians. Born in 1608 in Faenza to a family with limited means, his education was overseen by his uncle Jacopo, a Benedictine monk. He entered a Jesuit college in 1624 and, when Castelli moved to Rome in 1626, Torricelli spent the next six years as both Castelli's student and his secretary. From 1632 to 1641, Torricelli was secretary to Giovanni Ciampoli, another close friend of Galileo, and in 1641, three month's before Galileo's death, Torricelli joined Galileo as an assistant in Arcetri (across the Arno from Florence), where Galileo had been living under house arrest since his run-in with the Inquisition in 1633. After Galileo's death, Torricelli would go on to hold his position as court mathematician to the Medicis. Though he is now most famous for his discovery of barometric pressure, his only published work, the Opera Geometrica of 1644, which contained de Dimensione Parabolae and several other works, was very well regarded at the time. In particular, because Cavalieri's work on indivisibles was so difficult to understand, Torricelli's Opera Geometrica, and in particular Quadratura Parabolae per novam indivisibilium Geometriam pluribus modis absoluta, was often the source from which mathematicians learned about the method of indivisibles--hence its importance in the history of mathematics.
Andrew Leahy (Knox College), "A Translation of Evangelista Torricelli's Quadratura Parabolae - Some Historical Background," Convergence (February 2017)




