The Theorem that Won the War: Activities for Part 2.2 (Conjugates)

1. Find \(P\), the permutation that shifts letters one place forward (so \(a \rightarrow b\), \(b \rightarrow c\), and so on).  Also find \(P^{-1}\).
2. Prove:  \((P^{k}NP^{-k})^{-1} = P^{k}N^{-1}P^{-k}\).
3. Consider the following initial setup for an Enigma encryption:

   
   

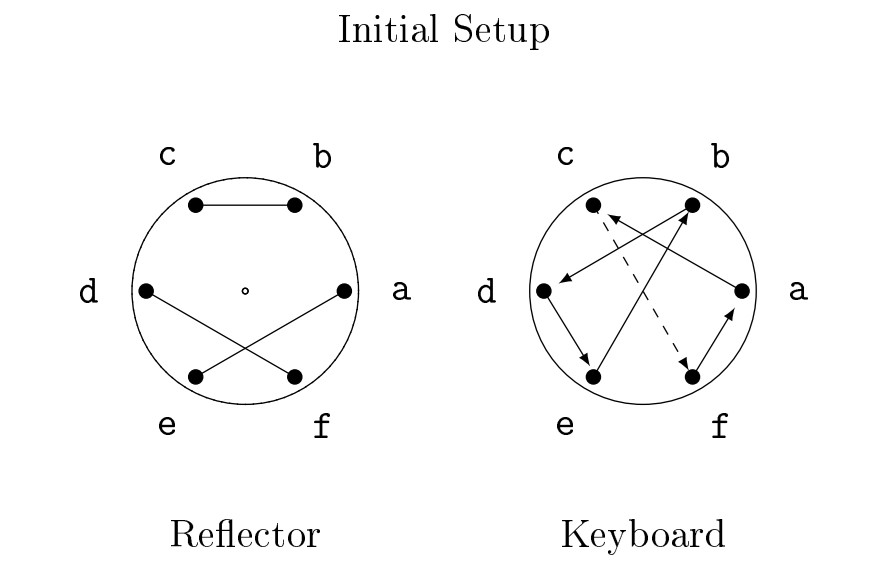
   1. Find \(Q\), the permutation corresponding to the reflector.
   2. Find \(N\), the permutation corresponding to the initial setup of the keyboard rotor. Also find \(N^{-1}\).
   3. Find the permutation \(P\) that shifts each letter one place forward (so \(a \rightarrow b\), \(b \rightarrow c\), and so on).
   4. Find the inverse permutation \(P^{-1}\).
   5. Compute \(PNP^{-1}\).
   6. Compute \(PN^{-1}P^{-1}\).
   7. Find \(E_{1}\), the permutation that will be used to encrypt the first letter.
   8. Verify \(E_{1} = PN^{-1}P^{-1} Q PNP^{-1}\).  (Remember, in our paper Enigma we're ignoring the permutation \(S\) associated with the plugboard.)
   9. Find \(E_{2}\) and \(E_{3}\).
4. The following explains the significance of the reflector. Using the reflector and keyboard setup shown above, answer the following.
   1. Consider an Enigma-type machine that omitted a rotor, so the \(k\)th letter of a message would use the permutation \(H_{k} = P^{k}NP^{-k}\).  Find \(H_{1}\) and \(H_{1}^{-1}\).
   2. Show that by including the reflector \(Q\), the \(k\)th letter of an Enigma message would use the permutation \(E_{k} = H_{k}^{-1}QH_{k}\).
   3. Find \(E_{1}\) and \(E_{1}^{-1}\).
   4. Why does the reflector make the Enigma encryption easier to use?

Return to the overview of Part 2.2 (Conjugates).

Continue to the overview of Part 2.3 (Cycle Notation).