Thomas Simpson and Maxima and Minima - Motion of bodies I

Two bodies move at the same time, from two given places A and B, and proceed uniformly from thence in given directions, AP and BQ, with celerities in a given ratio; it is proposed to find their position, and how far each has gone, when they are nearest possible to each other (Example XIII, page 28).

Let \(a = AC, b = BC, c = DC\) in the adjacent figure. Assume \(m\) is the velocity (“celerity”) of the body that moves in the direction \(AP\) while \(n\) is the velocity of the body that moves in the direction \(BN\).

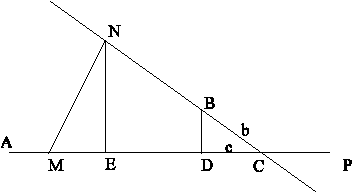
At time \(t\) the first body will be at \(M\) while the second body will be at \(N\) (Simpson calls these two points “cotemporary”). Next draw perpendiculars \(\overline{NE}\) and \(\overline{BD}\) to \(AP\), and let \(x = CN\). Since \(\triangle ECN\) is similar to \(\triangle DCB\), we can conclude that \(\frac{b}{x} = \frac{c}{CE}\). Because \(M\) and \(N\) are cotemporary points it follows that \(\frac{AM}{m} = \frac{BN}{n}\), therefore \(AM = \frac{m}{n}(x - b)\). So \(CM = AC - AM = a - \frac{m}{n}(x - b) = d - \frac{m}{n}x\), where \(d = a + \frac{m}{n}b\). By the law of cosines we have \(MN^2 = CM^2 + CN^2 - 2(CM)(CN)cosC\). But \(cosC = \frac{EC}{CN}\). Therefore

\(MN^2 = CM^2 + CN^2 - 2(CM)(CE) = (d - \frac{m}{n} x)^2 + x^2 - 2(d - \frac{m}{n} x) \frac{cx}{b}\)

\(= d^2 - (\frac{2dm}{n} - \frac{2cd}{b}) x + (\frac{m^2}{n^2} + \frac{2cm}{nb}) x^2\).

Taking the derivative of \(MN^2\), which is obviously a function of \(x\), and making it equal to zero we get

\(x = \frac{mnbd + cdn^2}{bm^2 + 2cmn}\)

This is the value where \(MN^2\), and consequently \(MN\), attains its minimum.

Remark: Maybe Simpson should have mentioned that \(MN^2\) is a second degree polynomial in the variable \(x\), thus on the Cartesian plane it represents a vertical parabola that opens upwards with minimum at \(-\frac{r}{2s}\) where \(r\) and \(s\) are the coefficients of \(x\) and \(x^2\) respectively. We would get exactly the same value obtained before, namely

\(x = \frac{mnbd + cdn^2}{bm^2 + 2cmn}\)

So, in this problem there is an alternative to the use of derivatives.

Editor’s Note: This article was published in 2005.