Thomas Simpson and Maxima and Minima - Maximizing the volume of a cone

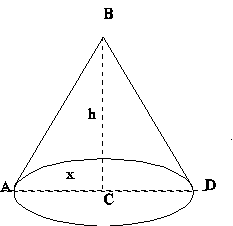
Of all cones under the same given superficies to find that (ABD) whose solidity is the greatest (Example IX, p. 21).

It should be noted that by “superficies” Simpson means “lateral surface”, while “solidity” is an archaic synonym of “volume”. We have \(s = \pi x^2 + \pi xy\), where \(s\) is the lateral surface, \(y\) is the length of the slant side, and \(x\) the radius of the base. Then \(y = \frac{s}{\pi x} - x\). The height \(h\) is found by using the Pythagorean proposition. Thus

\(h = \sqrt{(\frac{s}{\pi x} - x)^2 - x^2} = \sqrt{\frac{s^2}{\pi^2 x^2} - \frac{2s}{\pi}}\),

and consequently

\(V(x) = \frac{1}{3} \pi x^2 \sqrt{\frac{s^2}{\pi^2 x^2} - \frac{2s}{\pi}}\).

Define \(f(x) = \frac{s^2}{9}x^2 - \frac{2 \pi s}{9}x^4\), the square of the volume. Then \(0 = f'(x) = \frac{2s^2}{9}x - \frac{8}{9}\pi s x^3\) implies \(x = \sqrt{\frac{s}{4\pi}}\), which is the value of the radius at which the volume is the greatest. Under these circumstances

\(y = \frac{s - \pi x^2}{\pi x} = \frac{s - \frac{\pi s}{4 \pi}}{\pi \sqrt{\frac{s}{4 \pi}}}= 3\sqrt{\frac{s}{4 \pi}} = 3x \).

Remark: As in example IV, Simpson does not mention that the square of the volume is a biquadratic expression. There is a simple algebraic alternative to determine its maximum: define \(z = x^2\), thus the problem is reduced to finding the point where the parabola defined by \(-\frac{2 \pi s}{9} z^2 + \frac{s^2}{9} z\) attains its maximum. Given that this is a quadratic polynomial, we know that this takes place at

\(z = \frac{\frac{-s^2}{9}}{\frac{-4 \pi s}{9}}= \frac{s}{4 \pi}\),

thus \(x = \sqrt{\frac{s}{4 \pi}}\).

Editor's Note: This article was published in 2005.