Wibold's Ludus Regularis - Author's Puzzle - The Game Board - Relation to Rithmomachia

The Author's Puzzle

At the end of the text, the author's name is disguised by means of the following verse. Colvener, editor of Balderic’s Chronicon [2], stated that this literary device was commonly used by medieval writers.

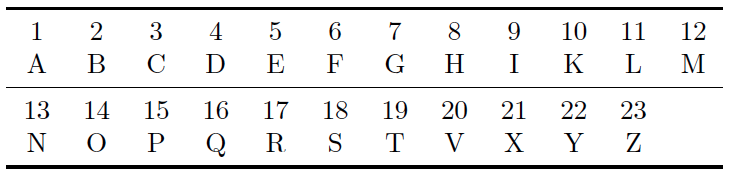
To solve the puzzle posed in the verse it is important to know that the Latin alphabet consists of only these 23 letters.

The name of the author is sought in these dactyls
If with numbers? Ten taken twice makes the first and the second,
And the eighth letter, and so with number nine
The third is thrown in, the fourth here to be the number two,
Four and ten the fifth, next finally number six
is read with the number eleven, twice two the seventh, as well as
The last in order limits in numbers thrice six.
To what has been brought together, the theoretical summit is dedicated
The virginity of the soul and the ten commandments, shine forth,
Which he who cares [for them] establishes for himself the delights of heaven.

This game advises the cleric to proceed to the gaming-table,
so that he may have the power to store up the names of the virtues.

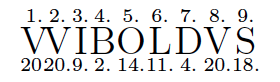
The Game Board

Was Wibold's game truly a board game? It seems that it must necessarily have been the case. Aside from the conjecture that Wibold was attempting to draw clerics away from the game of Tables, to which he would have desired some similarity, stronger reasons in favor are that a surface is required for casting the dice, the spelling of the virtues must be displayed, and there must be a way to mark ownership of virtues once they are acquired. Any game board for Ludus Regularis would have to display this information before the players in order to serve these purposes. George Colvener and his colleague Boëtius Epo proposed three game boards [2].

One of these, designed for a simplified version of play, arranges the virtues in a circle with a spinner in the center. The randomizing device is the spinner; all the dice are abandoned. Employing this device ignores most of Wibold's instructions since each of the 56 virtues arrives with equal probability. This game board of Colvener and Epo, which was included as a foldout in [2], is reproduced here as Figure 6 [5].

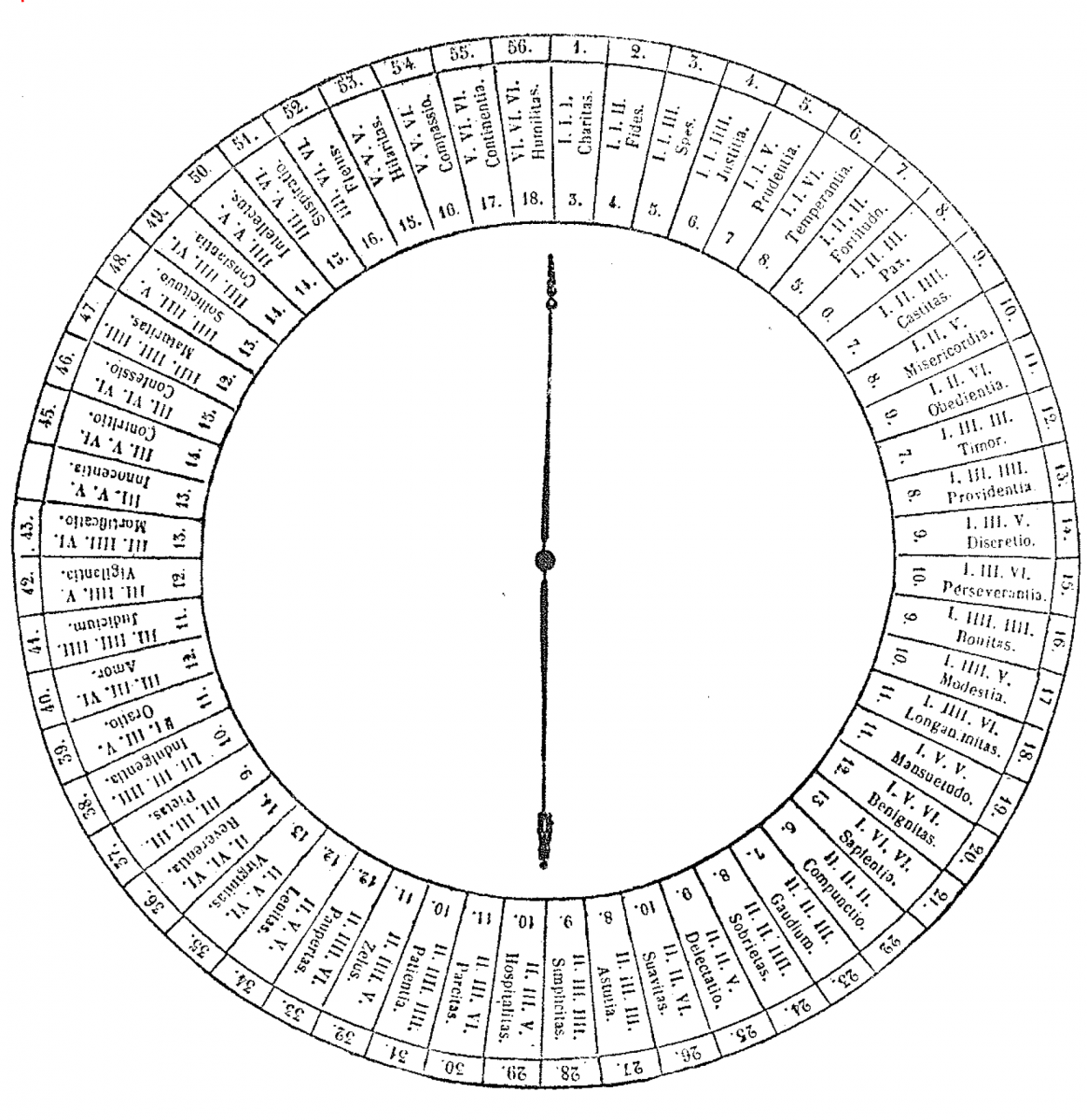
Figure 6. Colvener's proposed simplified game board (Courtesy of Xavier University Library)

The other two game boards proposed by Colvener and Epo [2] arrange the virtues in the same order as Table 1 within a rectangular border, much as on a modern Monopoly board. Although there are slight differences between the two, we offer the rectangular game board in Table 5 (see Possible Game Boards, next page), as an example of this type. Table 6 in Possible Game Boards (next page) is proposed by the authors as another alternative.

Relation to Rithmomachia

Is Ludus Regularis related to other games of its time? Le Glay stated in his notes on Wibold's text:

The game that he has invented has even some evident relationships with Rythmomachie, or philosophical game of Pythagoras, on which Claude Boissières has published a treatise, in octavo, 1556 [5].

The reference here is to a chess-like game known as the Philosopher's Game, or Rithmomachia – that is, (A)rithmomachia or “Battle of the Numbers" – from the Greek words arithmos and machē. Its origin was attributed to Pythagoras, as the name Rithmomachia also speaks to a Greek origin. The earliest written record we possess of it is a treatise by the monk Asilo of Würzburg dating from 1030. 

Rithmomachia is a game of strategy, whereas Wibold's game is one of pure chance. Rithmomachia is based on a theory of numbers somewhat sophisticated for that time; in Ludus regularis, the numbers are merely identifiers or, at most, the subject of arithmology. Moreover, Rithmomachia was not proscribed by authorities as was the game of Tables, due to the perceived moral hazard of dicing. For these reasons, we see little similarity between Rithmomachia and Ludus regularis with the following exception.

There is strong evidence that Rithmomachia was originally employed as a teaching tool to train its practitioners in the Nichomachian theory of numbers and that its popularity as a game came only centuries later. Similarly, Wibold promoted the playing of his game in order that the players “may have practice with the combination of numbers."

Thomas More described similar amusements in his Utopia of 1518. In Book II, Chapter IV we find a reference to Rithmomachia and a game similar to it involving a battle of virtues and vices.

Diceplaye, and suche other folish and pernicious games, they knowe not; but they use II games not muche unlike the chesse. The one is the battell of numbers, wherin one number stealethe awaye another. The other is wherin vices fyghte wyth vertues, as it were in battell array, or a set fyld. In the which game is verye properlye shewed bothe the striffe and discorde that vices haue amonge themselves, and agayne theire unitye and concorde againste vertues; and also what vices be repugnaunt to what virtues; and what powre and strenght they assaile them openlye; by what wieles and subteltye they assuate them secretelye; with what helpe and aide the vertues resiste, and ouercome the puissaunce of the vices; by what craft they frustate their purposes; and finally by what sleight or meanes the one getteth the victory. (See note 18.)

More's game mentioned above likewise bears no similarity to Wibold's. Wibold's game seems to be unique in its structure in that virtues (or properties) are acquired for the singular purpose of emulating them.

Note

18. Translated by Raphe Robynson, 1551 [14].