The Life of Sir Charles Scarburgh: Mathematical Treasure – The English Euclide

In 1705, a little over a decade after Sir Charles Scarburgh’s death, a new English translation of the first six books of the Elements—with extensive annotations and commentary—was published: The English Euclide.

Figure 7. Title page of The English Euclide. All images on this page provided courtesy of
the Internet Archive from its digitization of the copy owned by the Wellcome Library.

The author of the work is listed as Edmund Scarburgh, Sir Charles Scarburgh’s son. How much of the work was actually done by Edmund as opposed to his father is uncertain. Edmund wrote in the preface that the work “was design’d, and begun many years ago at the Command of my much Honored Father” and that his father “liv’d to have the perusal, and Correction of the greatest part of this Work” [Scarburgh 1705, 4]. While Edmund seems to be claiming to have done the majority of the new translation, with his father only selecting the task for him and making occasional editorial corrections to Edmund’s work, it seems possible that the project was actually started and perhaps even substantially completed by Sir Charles Scarburgh before his death. The large collection of translations and commentaries in Sir Charles Scarburgh’s library showed his own significant, lifelong interest in the Elements, and it is unclear why he would have settled the entire project of translation and annotation solely on his son.

There were certainly published claims that Sir Charles Scarburgh played a greater role in the production of the work, although such claims provided no supporting sources and often included incorrect details. For example, the biography of Sir Charles Scarburgh that appeared in the final volume of Biographia Britannica, published in 1766, contained the assertion that the new annotated translation was based on “his father’s manuscript” [Biographia Britannica 1766, 160], but misidentified the son who published the work as Charles rather than Edmund.

Figure 8. Page 27 of The English Euclide.

The first book opens with 34 definitions. For example, in Figure 8 shown above, Definition 24 defines a “equicrural” (that is, isosceles) triangle as one with only two equal sides.

Figure 9. Page 42 of The English Euclide.

The English Euclide then moves on to three postulates: between any two points can be drawn a straight line; any finite straight line can be extended; and with any center and distance a circle can be drawn. These are followed by 12 “Speculative Principles, Common Notions, or Axioms,” such as Axiom 10 shown in Figure 9 above: that all right angles are equal to one another.

Figure 10. Pages 59–60 of The English Euclide.

Figure 10 above shows the proof of the fifth proposition in Book I, that “equicrural” triangles have equal base angles, followed by the corollary that an equilateral triangle will have three equal angles.

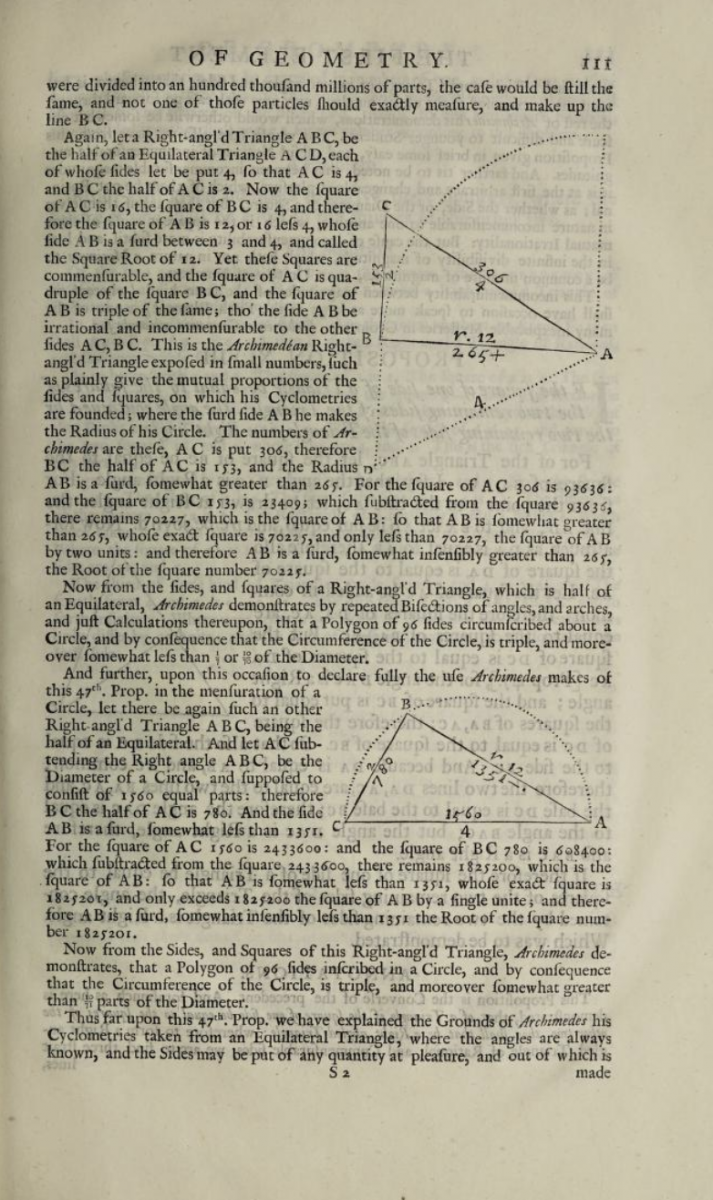
Figure 11. Page 111 of The English Euclide.

Proposition 47 of Book I is more commonly known as the Pythagorean Theorem. As shown in Figure 11 above, the annotations following this proposition contain several examples of the theorem using actual numbers.

Figure 12. Page 162 of The English Euclide.

Figure 12 above shows the fourth proposition of Book IV, inscribing a circle in an arbitrary triangle by constructing the angle bisectors.

Figure 13. Page 282 of The English Euclide.

On the final page of The English Euclide (see Figure 13 above) is a concluding epigram, written in both Greek and English.