- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Pitfalls and Potential Solutions to Your Primary Source Problems: This makes no sense at all.
You have the source and the language isn't a problem. It's the mathematics.
Example
I was working on a project to use primary sources to teach existence / uniqueness theorems for first-order differential equations. After some research, I was led to Peano's 1890 paper, “Démonstration de l’intégrabilité des équations différentielles ordinaires” [Peano 1890], which supposedly contained the correct proof of his existence theorem (he published the result with an incorrect proof earlier, in 1886). However, when I started looking through the paper, it was impossible (for me) to figure out what was happening, and it wasn’t because I couldn’t read French. The mathematics was entirely symbolic logic and was indecipherable to me. As near as I can tell, Figure 6 displays the statement of the theorem I was trying to teach.[18]

Figure 6. Peano’s existence theorem . . . I think [Peano 1890, p. 204].
Its proof is even more opaque, and I had no idea how to approach this primary source. I admit I was relieved to see that others had similar reactions to this passage. Fulvia Skof in Giuseppe Peano between Mathematics and Logic[19] wrote
It should be remarked that the strong defense of symbolic writing which characterizes his work as a whole contributed to win him the esteem he enjoys today in the mathematical community, and especially among logical mathematicians. But it was also an obstacle to the timely achievement of the success promised by Peano’s brilliant results in Analysis in the early years and by his innovative ideas; for the presentation of the results in ideographic form, distancing the majority of readers, in the end made them little known. This is what happened, for instance, to the important theorem on the existence of a solution to Cauchy’s problem for first-order differential equations and the subsequent extensions to systems [Skof 2008, p. 4] .
There is no way that this is an appropriate primary source for my class. But, can something be salvaged from it?
It may help to know that . . .
- The source might still have value. Though I obviously don't ask my students to understand Peano's symbolic writing, I do mention the story and show his version when presenting the theorem. It takes 20 seconds and does them no harm.
- Your confusion might not be your fault. It might be due to a typo, or because the passage is simply not true. Historically, there has been little oversight in scientific publication. Generally, the acceptance of a paper was at the discretion of the editor, or perhaps a small group of advisors. There was no guarantee that anyone deciding its acceptance was an expert, much less a mathematician, much less a scientist. Alex Csiszar noted
It was only near the turn of the twentieth century that the idea began to take hold that editors and referees, taken as one large machinery of judgment, ought to ensure the integrity of the scientific literature as a whole. . . . Outside the Anglophone scientific world, referee systems remained rare. Albert Einstein, for example, was shocked when an American journal sent a paper of his to a referee in 1932. The idea that any legitimate scientific journal ought to implement a formal referee system began to take hold in the decades following the Second World War [Csiszar 2016, p. 308].
Little oversight combined with tedious printing technology led to many mistakes and much confusion . . . not just yours.
- It might still be worth the trouble. And you should give your students some credit. Otero noted
But as I contemplated the audience I was planning to work with, I realized that these students are already quite accustomed to reading equally difficult original texts in their other humanities courses. After all, in philosophy courses they will often read Plato, Aristotle, Thomas Aquinas, Kant, Kierkegaard, Wittgenstein—in translation, of course, but otherwise unadulterated. In their literature courses they grapple with the works of Aristophanes, Dante, Shakespeare, Voltaire, Tolstoy, Joyce. What’s wrong with asking them to study some of the classics in mathematics, too? [Otero 1999, p. 60]
- You can look elsewhere. Others may have found the passages challenging and worked to clarify them, especially editors of collected works. Skof continued
Beppo Levi recalls, in his commemoration of his Master, that they were virtually unknown until the German mathematician Gustav Mie, in his “Beweis der Integrierbarkeit gewoehnlicher Differentialgleichungssysteme nach Peano,” based on Peano’s 1890 paper—with addition of a study of the uniqueness of the solution—supplied, as Levi says: . . . free re-exposition of Peano's Memoir . . . , freeing it from the new hindrance to reading caused by the use of logical ideography, which Peano had introduced in his own exposition, and from that prolixity that resulted from an excessive preciseness in the statement of introductory observations. It was only after Mie’s work that Peano’s result and his procedure to proof could be universally appreciated at its true value, and could prompt further studies by De La Valle-Poussin, Arzel, and Osgood [Skof 2008, p. 5].
- It’s possible that the mathematics may not be as difficult as it first appears and may just be notationally inconvenient or algebraically intensive. This is how my RK-4 PSP came to be [Parker 2021b]. The original article from Runge skipped a lot of steps, which made using it in the classroom very difficult. So, I had an undergraduate student translate and fill in all the gaps as an honors thesis.
- It might be best to pivot. Skof referenced the existence result of William Fogg Osgood (1864–1943). It, and the uniqueness result of Émile Picard (1856–1941), are both understandable and usable in the classroom. And, luckily, both are translated in [Calinger 1994]. See Figure 3.

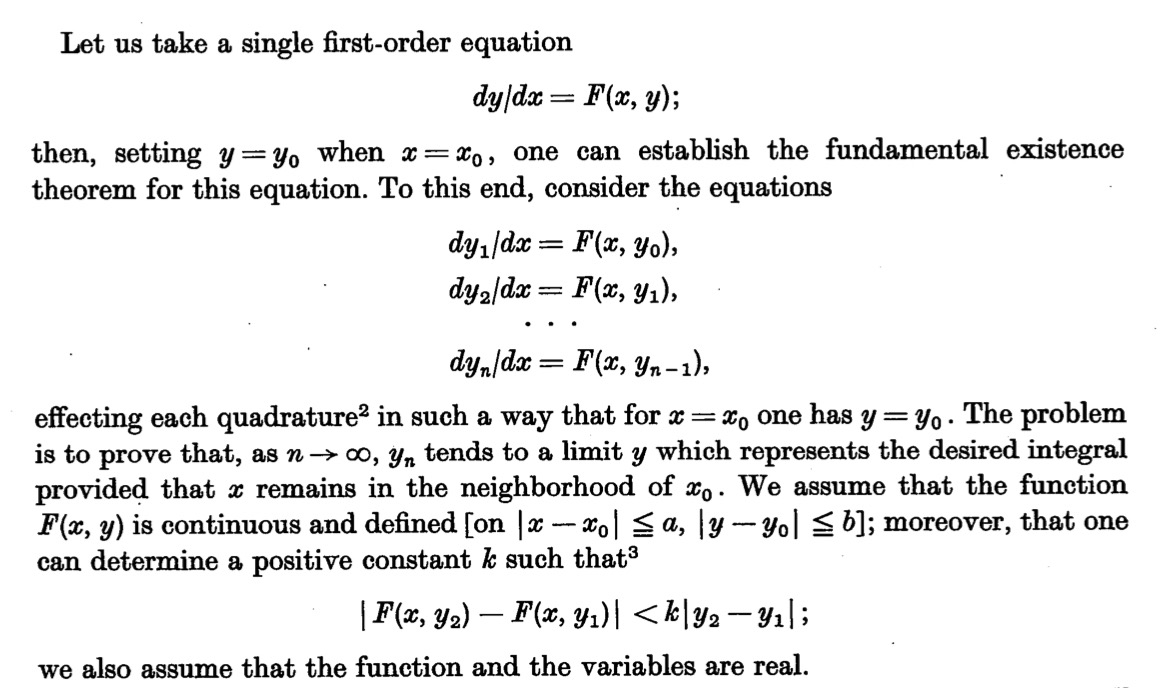
Figure 7. Osgood’s existence and Picard’s uniqueness theorems. Screenshots provided by author.
- It might be best to skip it altogether. Remember that the goal is to use primary sources that aid in the teaching and learning of mathematics. If a text doesn’t help with that, then it should not be used.
[18] I only think this because Peano’s note stated, “We can determine in the interval from \(0\) to \(1\) a complex function of the real variable \(t\) which vanishes for \(t=0\) and which satisfies the given differential equation on this interval.”
[19] Remember that biographies can be fertile ground for material.
Adam E. Parker (Wittenberg University), "Pitfalls and Potential Solutions to Your Primary Source Problems: This makes no sense at all.," Convergence (December 2023)




