- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Pantas’ Cabinet of Mathematical Wonders: Images and the History of Mathematics – Selecting Images – Ancient Artifacts
Appropriate computer searches reveal an abundance of images of instruments for measuring and computing; of people who contributed to mathematics; and of actual mathematical works, such as books and notes, that can be used to enrich mathematics teaching and learning [Kidwell 2021]. If known by name, they can be sought out; for example, images of the Ishango Tally Bone, the oldest existing human mathematics artifact, are available online, including as a “mathematical treasure” here in MAA Convergence. (See Figure 5.)

Figure 5. The Ishango tally bone is believed to be 20,000 to 25,000 years old. (Image presented courtesy of the Museum of Natural Sciences, Brussels, Belgium. You may use this image in your classroom; all other uses require permission from the Museum of Natural Sciences, Royal Belgian Institute of Natural Sciences.)
The age of the Ishango bone, 20,000–25,000 years, testifies to the long human involvement with mathematics and the need to record mathematical data. Conjectures about its function prepare the audience for a discussion of numeration in general. This can lead to the topic of tally sticks, and the rather interesting and amusing story of the British Exchequer’s Office 1826 fire. Due to the office’s disposal of centuries of accumulated tally sticks by burning, the House of Lords was set afire and burned down.
A very effective and information-laden image which has appeared in several books on the history of mathematics is Yale Babylonian Cuneiform 7289 (YBC 7289), a cuneiform tablet from the Old Babylonian period (circa 1900–1600 BCE). (See Figure 6.)
 |
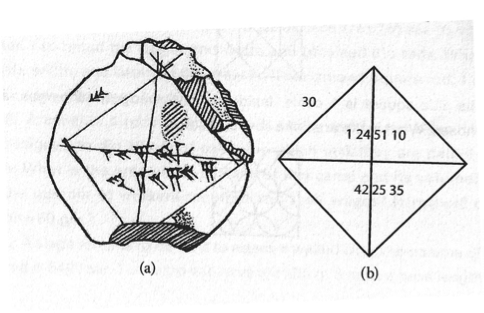 |
Figure 6. The clay "palm tablet" shown above, left, would fit in the hand of an ancient Mesopotamian scribe. A transcription and a translation are shown at right. (Image at left presented courtesy of the Yale Babylonian Collection. You may use this image in your classroom; all other uses require permission from the Yale Babylonian Collection. Images at right appear on p. 27 of the book by Asger Aaboe [1998/1964] and are reproduced here courtesy of the Mathematical Association of America.)
First, one notes the physical size of the clay tablet. It fits into a man’s hand, and indeed it was a palm tablet, held conveniently in the palm of one hand while the scribe, using his other hand, wrote on it. Modern students visualize cuneiform clay tables as being quite large—perhaps they are influenced by the stylized biblical illustrations of Moses holding the tablets of the Judeo-Christian Ten Commandments. But the most striking feature to the novice viewer is that the diagram clearly shows a square with its diagonals. Yes, the ancient Babylonians drew accurate geometric diagrams in clay as part of their mathematical discussions. Once, when I offered this illustration in an article for publication, I was challenged by the journal’s editor, who suspected I had drawn the diagram myself and was falsely attributing its origins to the Babylonians. Even very sophisticated people do not appreciate the fact that ancient mathematicians drew geometric diagrams to assist in problem solving.
Next, a deciphering of the cuneiform inscription reveals two numbers in sexagesimal notation: what we know as \(\sqrt 2\) and \(\sqrt 2\times 30,\) where \(30\) is the specified length of the side of the square. (See Figure 6b.) At this point in the inspection, two implications emerge:
- that at this early period before the rise of Greece and the Pythagoreans, the Babylonians possessed what we generally know as “the Pythagorean Theorem,” and
- that these ancient people could extract the square root of a number to several decimal places of accuracy.
Another obvious question then arises: “How did they do it?” Furthermore, if one looks closely at the image, one can see the “telltale” human fingerprint!
In addition to the book by Aaboe, images and discussion of this tablet appear in textbooks, including Burton [1997, p. 77] and Hodgkin [2005, p. 25].
Frank J. Swetz (The Pennsylvania State University), "Pantas’ Cabinet of Mathematical Wonders: Images and the History of Mathematics – Selecting Images – Ancient Artifacts," Convergence (May 2015), DOI:10.4169/convergence20150502




