- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Education at West Point: The First Hundred Years - Hutton and the Notebooks
The Hutton text was used at West Point for two decades, until 1823. At the time it was the best text to be had. The first of the two volumes consists of 533 pages. The main topics are arithmetic, logarithms, algebra, and geometry. The second volume deals with trigonometry and fluxions, in 622 pages. While this may not sound like very advanced mathematics, its level was far above what was taught at Harvard and other schools. American schools at the time taught a classical curriculum, consisting primarily of the classical languages and authors. West Point was the first school to teach a highly technical curriculum that prepared its students to be engineers.
We have information about how the Hutton book was used from student notebooks of the time. One such notebook in the USMA Archives is a 39-page notebook that belonged to Abraham Wendell.[1] He was from the State of New York and attended West Point from September 2, 1813 until March 2, 1815, when he graduated. At the time there was no set program or graduation requirements. Cadets were graduated when the professors felt they had obtained the requisite knowledge. Thus students that had prior college experience were often graduated within a year or two of coming to the Academy.
The notebook bears the signature “Abra: Wendell, West Point June 17th 1814.” This copybook deals with algebra and geometry. Specific topics include “Sir Isaac Newton's Rule for raising a Binomial to any power whatsoever,” “Infinite Series,” “Arithmetical Proportion,” “Application of Arithmetical Progression to Military Affairs,” “Of Computing Shot and Shells in a Finished Pile,” “Quadratic Equations,” and “Resolution of Cubic and Higher Equations.”
Also in the archives are two folders of materials relating to Henry W. Griswold who also graduated from West Point on March 2, 1815. There is a geometry notebook and two trigonometry notebooks.[2] The geometry manuscript, which is 12 pages long, contains 52 propositions of Euclidean geometry, but only the enunciations of the theorems; there are no proofs. There are diagrams for the first 31 of these theorems, and spaces for the remaining diagrams, but they were never drawn into this notebook. These theorems correspond exactly to the propositions in the 1812 edition of the first volume of Hutton.
The first of the trigonometry notebooks consists of 18 pages of carefully written notes. There are two pages of definitions followed by five pages of problems. Then there are three pages devoted to “Heights and Distances,” which include some lovely watercolor drawings, and eight pages of spherical trigonometry. There is a trigonometry problem in one of the notebooks that asks the cadet to calculate the height of Fort Clinton at West Point given information about the level of the Hudson river below. This is the only problem not taken directly from the text.
The second notebook is similar, however the writing is different, and though this notebook is catalogued with the Wendell papers, his name does not appear in it. The material covered is similar, but not the same, though still taken directly from Hutton. We believe that this may be the notebook of a cadet a year or so ahead of Wendell, and given to him to study from when the owner no longer needed it.[3] Since so much emphasis was placed on accurate, clean drawings, it would not be surprising if cadets who made good drawings loaned their work to other cadets. The following comment was made by Professor Albert Church (USMA class of 1828) just days before his death at a meeting of the United States Service Institute, 1864.
Of course, the real teachers in these subjects were those cadets who made careful notes, finished their drawings early in the day, made the demonstrations to their classmates, and lent their drawings for copying. Great skill was acquired in making these copies. A clear and large pane of glass was placed on the top of the washstand, a lighted candle underneath the finished drawing on the glass, and the paper for the copy on top, and every point quickly marked with a pencil.[4]
Both the Wendell and the Griswold notebooks can be precisely matched up with Hutton’s text.

Page from Hutton

Griswold Notebook
They contain the same peculiarities of language, bizarre capitalization, and choices of special cases for the diagrams. Thus it seems that the instructor had a copy of A Course in Mathematics in his hands and dictated or wrote out on the board the various propositions, while the cadets copied them down verbatim and then returned to their rooms to prepare a good copy in their notebooks. On Sunday mornings the cadets had to show their manuscripts to Professor Ellicott. “No questions were by way of examination asked as to how the results were obtained, but if our manuscripts were neat and presentable we were patted on the head and treated like good little boys. Of course we gave ourselves up to chirography rather than to the mastering of arithmetic.”[5] The trigonometry notebooks do not follow Hutton as closely as the geometry notebooks do, only covering portions of the text. For the most part, few proofs are provided. The notebooks contain largely propositions and examples.

A second Griswold notebook
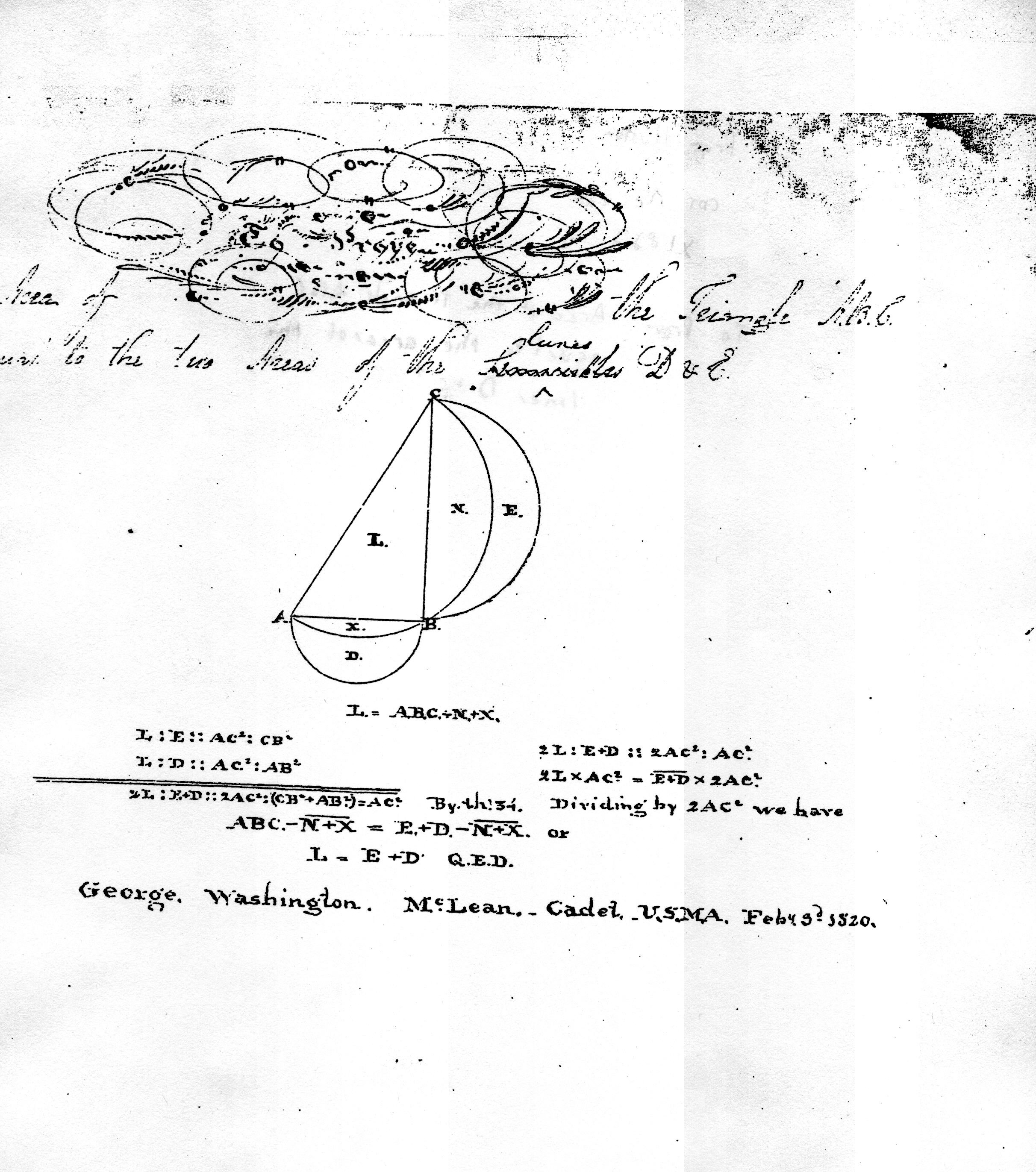
McLean notebook
[1]Wendell and Griswald notebooks, USMA Special Collections.
[2]We would like to thank Christine E. Coalwell, Research Associate at Monticello, The Thomas Jefferson Memorial Foundation, for calling these three notebooks to our attention.
[3]This tradition is still maintained at the Academy. After completing the core mathematics courses, each cadet passes their math portfolio on to the Plebe they are in charge of.
[4]Annual Report of the Superintendent of the United States Military Academy, Washington, 1896, p. 61.
[5]George D. Ramsay, “Recollections of the U. S. Military Academy at West Point, New York, 1814-1820,” typescript in West Point archives. This is paraphrased in George W. Cullum, “The Early History of the United States Military Academy,” pp. 465-672 of volume 3 of his Biographical Register of the Officers and Graduates of the U. S. Military Academy, 1891, esp. p. 621.
Editor's note: This article was published in May of 2008.
V. Frederick Rickey and Amy Shell-Gellasch, "Mathematics Education at West Point: The First Hundred Years - Hutton and the Notebooks," Convergence (July 2010)




