Mathematics as the Science of Patterns - Euclid

Book III of Euclid’s Elements concerns the basic properties of circles, for example, that one can always find the center of a given circle (proposition 1); that a line through the center  is perpendicular to a chord if and only if it bisects the chord (proposition 3); that two circles can intersect one another in at most two points (proposition 10); that the diameter is the greatest chord (proposition 15); that a line is tangent to a circle if and only if it is perpendicular to a radius through the point of contact (propositions 18, 19); that the sum of the opposite angles of an inscribed quadrilateral is equal to two right angles (proposition 22); that the angle in a semicircle is right (proposition 31).   Proposition 35 is the proposition stated above, namely:

If in a circle two straight lines cut each other, the rectangle contained by the segments of the one is equal to the rectangle contained by the segments of the other. 

Proposition 36 tells us, in addition:

If a point is taken outside the circle, and from it two lines fall on the circle, one cutting the circle and the other tangent, then the rectangle contained by whole of the line cutting the circle and the part of it intercepted outside the circle between the point and the convex circumference will be equal to the square on the tangent.

Proposition 37, which ends the book, is the converse of Proposition 36, providing a criterion for concluding when a line from a point outside a circle will be tangent to the circle.     

        The demonstration of proposition 35, which I shall present in a moment, is well worth seeing since Euclid’s approach is different than the usual classroom approach via similarity; indeed, Euclid does not treat similarity at all until the sixth book of the Elements.  Before that, though, the reader ought to know why I go to pains to avoid the usual “product of the lengths of two segments” and insist on saying “the rectangle contained by two segments.”  First of all, this is the way Euclid says it.  And if one is dealing with history, one ought to be sensitive to the way things are put.  Second, Euclid really means “the rectangle contained by two segments”; for Euclid, multiplication (pollaplēsios in Greek) is reserved for numbers, and ‘numbers’, for him, means only natural numbers.  That a rectangle, for Euclid, is a rectangle and square a square is crucial when one considers propositions such as this from Book II of the Elements:

If a straight line be cut into equal and unequal segments the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half (Book II, proposition 5).

Thus if AB is bisected at C and divided again at D (see fig. 1), then Euclid says the rectangle contained by AD and DB (which I shall abbreviate hereafter as rect.AD,DB) together with the square on CD (which I shall abbreviate hereafter sq.CD) is equal to sq. CB. With CZ being the square built on CB, BE being joined, and KM and DH being drawn parallel to AB and BZ, respectively, Euclid must show that rectangle AQ together with the square LH is equal to the square CZ; once one realizes that AQ is equal to the figure CBZHQL, the proof becomes, with all the squares and rectangles in plain view, almost a ‘proof-without-words’.  

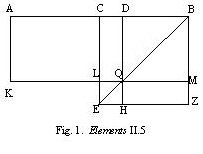
Taking AC=a and CD=b, this proposition has been understood in the past to show, in geometric language, the algebraic identity (a+b)(a-b)+b²=a², or, in its more familiar form, (a+b)(a-b)=a²-b².   For someone who already knows algebra and knows its importance in modern mathematics, this is a very seductive interpretation.  The problem is that while the interpretation makes sense mathematically it really does not hold water historically, as I described above (see Fried & Unguru, 2001 for a discussion of this proposition in particular).  But let us leave that issue and return to Euclid’s proof (slightly paraphrased) of III.35, which, incidentally, relies on the proposition just cited!