- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasure: Cyffer-Boek of Jan Coutereels
Little is known of Jan Coutereels other than that he had his own “French School,” a school that included the French language in its curriculum, in the Dutch city of Middleburg and that he was an active Dutch reckoning master and author of several books on business arithmetic written during the period 1596-1624. His Cyffer-Boek (Cipher Book) of 1690 is typical of his efforts.

The frontispiece for the book pictures an active merchants’ guild house in Utrecht. The long table seems to be lined with accountants busy with their calculations, while at the head table, the master merchants plan future ventures assisted by scientific instruments, including a globe.

Page 2 considers “Numeration,” the writing and reading of the “Hindu-Arabic” numbers. Note that “a million” is defined to be “a thousand times a thousand.” In the system, the largest number listed is “a thousand times a thousand million,” our “trillion.”

Page 3 continues with practice in the reading of numerals and then introduces “Addition.” It is assumed the reader is familiar with the basic addition facts. Column addition of same-length numbers is undertaken with the condition that only quantities with like units be added: pounds to pounds (weight); guilders to guilders (money); ells to ells (cloth measure); etc.

On page 8, our Dutch author presented two algorithms for the multiplication of two multi-digit numbers. At the top of the page, two products are obtained using a variation of the Italian “per saccheri” method, which had by that time become popular and remains so today. An interesting algorithm involving the configurations of a circle and a square is then demonstrated to obtain the product of two three-digit numbers. Can you determine just how it works? Would it work for numbers with more digits?

Page 9 gives a demonstration employing a square to obtain the product of two five-digit numbers. Again, do you understand how this algorithm functions? Will it work for any two five-digit numbers?
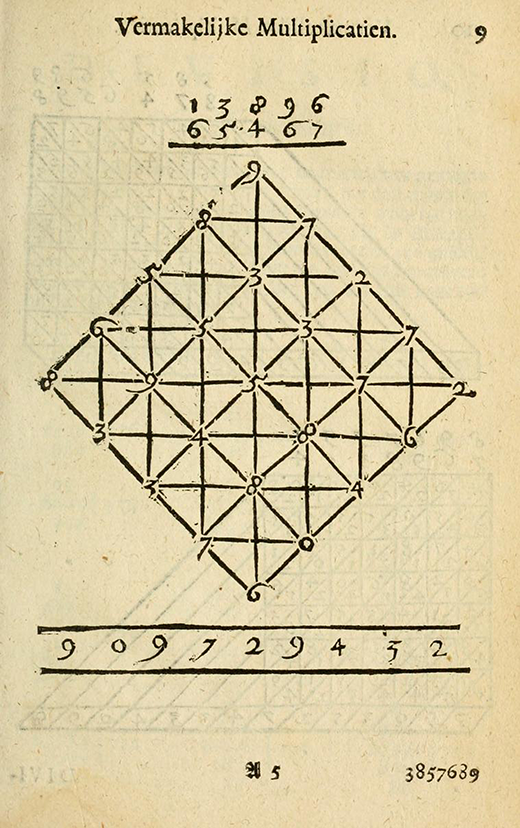
On page 10, a variation of the “gelosia” or lattice method of performing multiplication is illustrated. In the standard, more widely accepted application of gelosia multiplication, the multiplicand is written across the top of the square and the multiplier along the side, with the product then read on the remaining two sides. Is this “Dutch technique” better?

The “Rule of Three” is introduced on page 64.

On page 120, we find a discussion of fractions, or Gebroken (broken numbers), including their names and numerical symbols.

On page 121, the author discussed the “abbreviation” or reduction of fractions. In the first example given, 8/12 is reduced to 2/3. Here, a schematic approach is used whereby the common factor 4 is displayed atop a vertical bar. This pedagogical device is then applied in the remaining examples.

The addition of fractions is covered on page 126. The first example is “½ + ¾ makes 1¼.” Follow the algorithm as given. Is it mathematically correct?

This material is obtained through the courtesy of the University of California Libraries. A complete digital copy can be read on the UC Libraries’ Internet Archive.
Frank J. Swetz (The Pennsylvania State University), "Mathematical Treasure: Cyffer-Boek of Jan Coutereels," Convergence (May 2017)




