Led Astray by a Right Triangle: Misconception, Epiphany, and Redemption - Background

Background

Fifty years ago, when I first viewed the contents of the Chinese mathematical classic, Jiuzhang suanshu [Nine Chapters on the Mathematical Art] (ca. 100 BCE), I was impressed by the scope and depth of its mathematics and confounded that a work of such caliber remained almost completely unrecognized in the western world for so long. By incorporating the number “Nine” into the title of this work, the unknown author or authors were indicating that they thought the work to be comprehensive of the mathematical knowledge possessed at their time. In the numerology of ancient China, nine indicated completeness. The Nine Chapters show that Chinese mathematicians of this early period possessed an advanced decimal, place-value, system of numeration; recognized negative numbers; performed fractional operations with great proficiency; extracted roots of numbers; possessed correct area and volume formulae for a variety of area and volume computations; employed a “matrix” technique of computation for solving systems of linear equations; developed a high proficiency in applying “the rule of three” in solution schemes; and could perform geometric solutions involving applications of the “Pythagorean Theorem.” Further, the book’s well-organized collection of 246 mathematical problems distinguishes it, in my opinion, as the most comprehensive, extant testament to early problem solving. The Jiuzhang, within its nine chapters, had a story to tell and I sought to unravel, understand, and learn from it. (Since this initial encounter, an English language translation of the Nine Chapters has appeared [8].)

In my examination, I was particularly attracted to several mathematical features of this work: the Chinese algebraic versatility in applying the rule of three (Chapter 2, Millet and Rice); their matrix-like solution techniques for solving systems of linear equations, including those resulting in indeterminate solutions (Chapter 8, Rectangular Arrays); and their facility with right triangle applications (Chapter 9, Right Triangles). Assisted by a Chinese language translator, T. I. Kao, I ventured to obtain an English language version of the ninth chapter, Gougu [Right Triangles], a treatise in itself consisting of 24 problems involving right triangle theory and its applications to surveying and distance reckoning exercises. This effort, including my analysis and conclusions, was eventually published for a broader reading audience [12]. Whereas the Jiuzhang contains a compilation of Chinese mathematical practice actually employed centuries before the appearance of the book, it was apparent to me that the Chinese knowledge of the “Pythagorean Theorem” was developed and perfected independently, without foreign influences. Indeed the Chinese possessed an indigenous name for this relationship, the “Gougu rule,” and derived a geometric-algebraic proof, the Xian thu, for its validity. This is illustrated in Figure 1, below.

In the Chinese mathematical terminology of this time: gu was the longer leg of a right triangle; gou was the shorter leg. The Chinese characters for these terms were originally used to designate “thigh” and “leg.” The hypotenuse of the triangle was referred to as xian, which in a nonmathematical context referred to a string tightly strung between two points, such as a lute string. This analogy provides a clue as to how ancient peoples physically measured the length of an hypotenuse. The Xian thu, or hypotenuse diagram, shows a large square composed of four congruent “3-4-5” right triangles and a small center square set against a grid system. As depicted in the lefthand diagram in Figure 1, the side of the large square is an hypotenuse of measure \(5,\) therefore the area of the square is \(25\) square units, \(5^2.\) Now if the Xian thu is dissected and its regions rearranged into two smaller squares, as shown in the righthand diagram in Figure 1, it is seen that that the sum of their areas is \(3^2 + 4^2 = 25.\) This demonstration was generalized to prove that \[{\textit{gu}}^2 + {\textit{gou}}^2 = {\textit{xian}}^2,\] known as the “Gougu rule.”

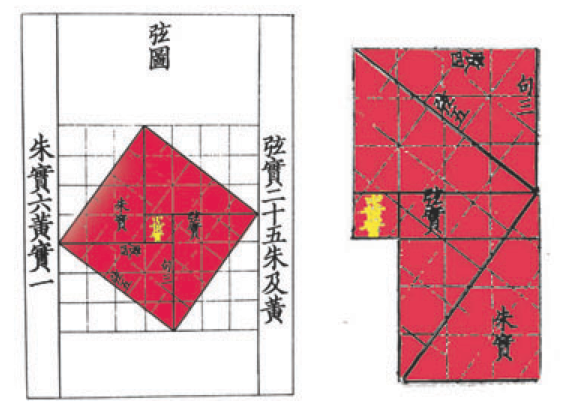
Figure 1. The Xian thu, or hypotenuse diagram, can be dissected to demonstrate the “Gougu rule,” or, as it is known in the West, the Pythagorean Theorem.

The concept of the right triangle was even embedded in Chinese myths on the origins of mathematics, as evident in a conversation in the Zhoubi suanjing [Mathematical Classic of the Zhou Gnomon], another extant second century BCE mathematical and astronomical classic [2]. In a fanciful conversation between Zhou Gong, a duke of the Zhou dynasty (ca. 1030-221 BCE), and the Grand Prefect Shang Gao, the Duke queried the old man endeavoring to learn the secrets of mathematics. Complimenting the Grand Prefect on his knowledge of mathematics, he inquired how the legendary patron of all Chinese knowledge, Fuxi (ca. 3000 BCE), could possibly obtain a mathematical understanding of the universe since “there are no steps to ascend the heavens and the earth is not measurable with a foot rule.”

The Prefect responded: “The art of numbering [mathematics] proceeds from the circle and the square.” (This statement may be purely metaphorical, as, for the ancient Chinese, the earth was symbolically represented by a square and the universe by a circle; thus perhaps Shang’s words were implying that mathematics is acquired from the physical realm.) He then continued: “The circle is derived from the square and the square from the rectangle.” [Here, “rectangle” is literally “the carpenter’s L-shaped square” or “set-square.”] His explanation proceeded, further elaborating on the importance of the right angle and included a Xian thu derivation [literally, “the hypotenuse diagram”] for the Gougu rule (see Figure 1, above).

		Alignment	Height	Depth	Distance

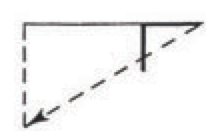
Figure 2. Uses of the set-square included forming right angles to align structures, and measuring heights, depths, and distances.

Zhou responded: “Great indeed is the art of numbering [mathematics]. I would like to ask the Dao [way, or method] of the use of the right-angled triangle [set-square].” To which Shang explained that the set-square placed on the ground helps to lay out structures, the set-square set on edge could be employed to observe heights, and reversed it could serve “to fathom depths.” Laid flat on the ground, the set-square was used for ascertaining distances, and rotated it could prescribe circles. See Figure 2, above. The Prefect ended his instruction by summarizing [6]:

He who understands the earth is a wise man, and he who understands the heavens is a sage. Knowledge is derived from the straight line. The straight line is derived from the right angle. And the combination of the right angle with numbers is what guides and rules the ten thousand things [meaning “everything”].

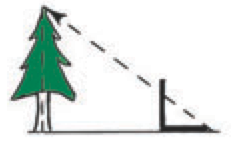
Such a prolonged discussion focused on the importance of the right triangle and its concrete template, the set-square, affirms the scientific and mathematical importance of right angled theory for the Early Chinese Empire. Reverence for the right triangle and the set square is further reinforced by a depiction on a tomb dated to the Han dynasty (ca. 200 BCE) showing Fuxi passing on his instrument of power and knowledge, the set square, to his consort, Nuwa; this divine couple are credited by the Chinese for bringing order to the universe. See Figure 3, below.

Figure 3. A tomb dated to the Han dynasty (ca. 200 BCE) shows the divine couple, Nuwa and Fuxi, sharing an instrument of power and knowledge, the set square.

In reflecting on these passages, the obvious, but often unrecognized, appreciation and utilization of the phenomena of perpendicularity by ancient peoples becomes obvious. Most likely, a primary mathematical instrument employed by humans was a simple vertical staff embedded into the ground, a gnomon. The actual placement of the staff would imitate the observed efficiency of nature such as a tree rising perpendicular to the plane of the ground. The staff would be placed perpendicular to the ground, it would “stand straight,” and the concept of vertical to horizontal would be preserved. In 1973, Jacob Bronowski, mathematician and noted philosopher of science, in writing on the place of science in human development, commented on how perpendicularity and its mathematical expression as contained in the “Pythagorean Theorem” described “the exact laws that bind the universe” and noted that its inscription had, appropriately, been considered for use in a message on a NASA Pioneer space probe as a topic of communication to other possible intelligent beings in the universe [1]. It appears, however, that it was never used.

Eventually, humans would design other tools to readily obtain this relationship: the plumb line for insuring the vertical and the surface level for the horizontal. The right angle itself would be captured in the “L” shaped design of a set-square. The use of two such sighting staffs set a distance apart allowed for the construction of straight lines. Sighting on such gnomons would eventually advance in their focus from near points to distant points, one perhaps elevated, and a slanted line of sight would be required and obtain significance. Now, a slanted sight line would allow the positional referencing of heavenly bodies, including the sun. A primitive astronomy was established and an intuitive concept of angle obtained. As a body higher in the sky was observed using a gnomon, the ray of the line of sight increased its upward slant and the angle with the horizontal increased. For the sun, this reckoning involved a shadow, a length easily observed and recorded. Such visual reckonings became important as temporal markers for the needs of agricultural societies and those that depended on the migrations of animal herds. Ancient societies kept chronological “shadow tables” [2, p. 196]. Pliny the Elder (23-79 CE), in his encyclopedic history of the ancient world, mentioned Thales employing shadow reckoning in Egypt. Plutarch, writing a few years later, also repeated this incident [7]:

Although he [the Pharaoh of Egypt] admired you [Thales] for other things, yet he particularly liked the manner by which you measured the height of the pyramid without any trouble or instrument; for, by merely placing your staff at the extremity of the shadow which the pyramid casts, you formed, by the impact of the sun’s rays, two triangles and so showed that the height of the pyramid was to the length of the staff in the same ratio as their respective shadows.

Evidence of such shadow reckoning can be found in most ancient societies. Shadow reckoning employing gnomons became a mathematical technique that embedded itself in the later designs of such instruments, such as the sun dial, astrolabe, quadrant, and eventually the nautical sextant. The ratio of gnomon length to its shadow length is now recognized as the cotangent of the intercepted angle. Indeed, a strong case can be made for shadow reckoning as the precursor of trigonometry [10].