- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
HoM Toolbox, or Historiography and Methodology for Mathematicians: Introduction – How Do We Create History?
You have chosen a topic in the history of mathematics, perhaps read some tertiary sources to get a sense of the background and scope of what you want to find out about that topic, identified relevant primary and secondary sources, and gathered information and ideas from those sources—carefully noting the citation for each tidbit, of course, because you want to be just as reliable and professional as the authors of your secondary sources. Whew! This is where my students would suggest it was time for pizza and a tasty beverage, and they would groan audibly when I would grin and point out the hard work was just beginning. (My courses were in fact all online, but it is impressive how these reactions can nonetheless be transmitted electronically.) It is tempting to remain in the research stage indefinitely, but at some point every historian has to start writing. That is when efforts to interpret the evidence begin in earnest, as historians return to the W and H questions that led to their research projects.
Addressing those pesky “how?” and “why?” questions about the past usually requires historians to contemplate two fundamental patterns in human activity:
- change and continuity over time;
- the causes, courses, and consequences of historical events.
The concepts of causation and change help us understand what happened and explain why those happenings were historically significant—in other words, why we should remember those events and note their influence on subsequent incidents. Historians summarize their understandings and explanations in a thesis statement; they then expand their understandings and explanations into a fully-developed argument grounded in historical evidence and sound reasoning. I have already mentioned several excellent guides to constructing a historical argument [e.g., Cronon 2008–2009 and Rael 2004; alternative options include Schrag 2007–2022, whose “Organization” section is particularly strong; Brown n.d.; Conolly-Smith 2007; Storey 2020; and Booth, Colomb, and Williams 2016]. Here, we will focus on how the decisions historians make about causation and change inform their theoretical approaches to analyzing and interpreting the past.
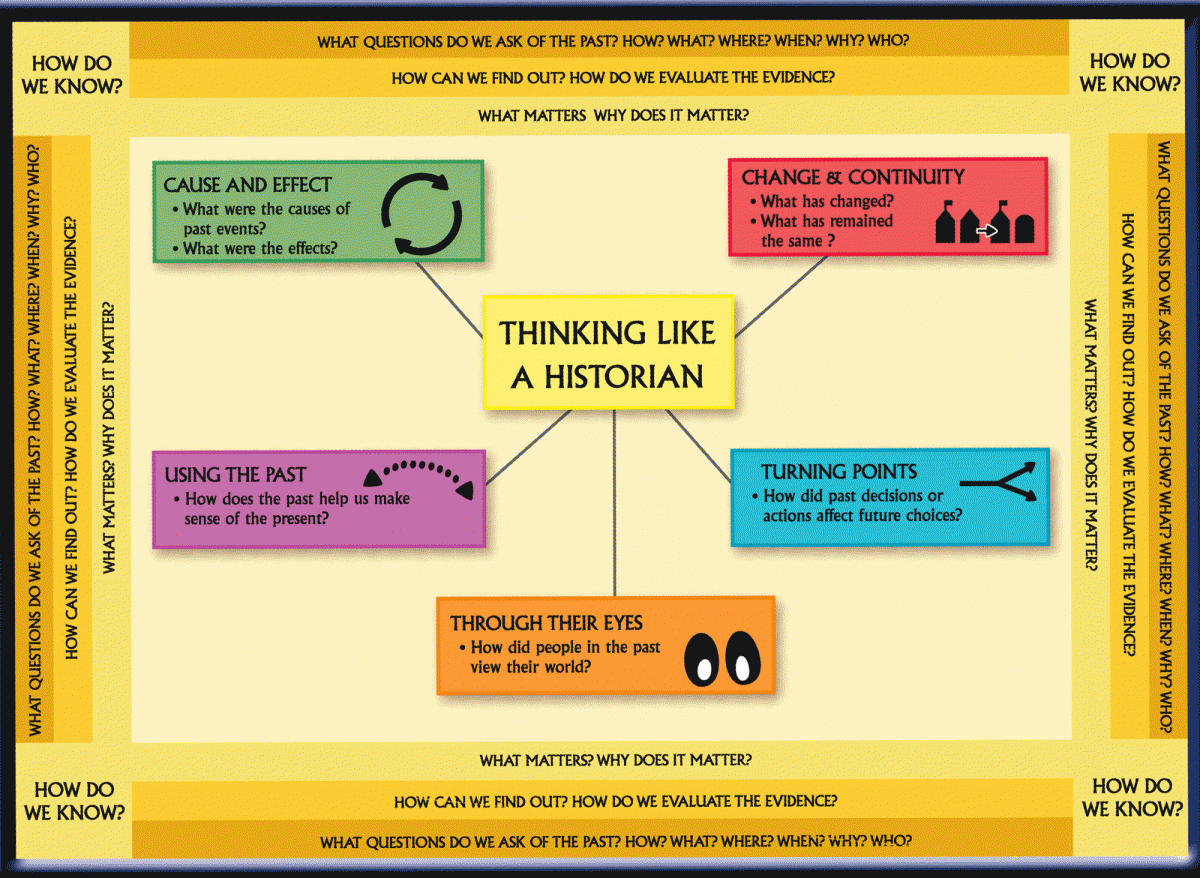
Figure 8. A chart depicting major components of historical thinking, developed on behalf of the Wisconsin Historical Society for elementary and secondary students and teachers by Nikki Mandell and Bobbie Malone [2007].
In history, “theoretical approach” is a term that denotes a conceptual lens or framework through which a historian views, understands, and draws conclusions about historical evidence—and, in turn, about causation and change. Since we are all shaped by our own experiences, education, and personal preferences, different historians may zero in on different aspects of the past and argue for the central importance of those aspects in creating causation and change. Those different perspectives denote different theoretical approaches. In other words, theoretical approaches are how historians get to their interpretations, not the end result of their research and not a guess about what happened in the past. Although there feasibly could be as many different theoretical approaches as there are historians, in practice historians tend to group by similar approaches into “schools” of historical interpretation. That simply means those historians hold similar ideas about what history is and how it ought to be researched. Some schools you may have heard about include Empirical approaches to historical interpretation, Marxist approaches, the Annales School, or Postmodernism. If you have attended history of math talks at an academic conference, you may have heard speakers criticizing “Whiggish” approaches to historical interpretation. If you would like to learn more about how theoretical approaches are central to the professional practice of history and find brief discussions of some of the major schools, see Gabrielle Spiegel’s 2008 presidential address to the American Historical Association [2009]. (More in-depth studies are provided by the readers mentioned earlier, [Green and Troup 2016; Tosh 2018].) In the next section, we will trace the development of some of the theoretical approaches that have been influential in the history of mathematics.
Amy Ackerberg-Hastings (MAA Convergence), "HoM Toolbox, or Historiography and Methodology for Mathematicians: Introduction – How Do We Create History?," Convergence (December 2022)




