Extending al-Karaji's Work on Sums of Odd Powers of Integers - The Sum of the Fifth Powers

Vidinli then asks, “What happens if we apply the same procedure to find the differences of third powers of \(S_n\)?” His answer consists of the following work: \begin{align} S_n^{\,3} - S_{n-1}^{\,\,3} &= {\bigg[ {\frac{n(n+1)}{2}}\bigg]}^3 - {\bigg[ {\frac{(n-1)n}{2}}\bigg]}^3 \\ &= {\frac{n^3}{8}} \Big({(n+1)}^3 - {(n-1)}^3 \Big) \\ &= {\frac{n^3}{8}}(n^3 + 3n^2 + 3n +1 - n^3 + 3n^2 - 3n + 1) \\ &= {\frac{n^3}{8}}(6n^2 + 2) \\ &= {\frac{1}{4}}(3n^5 + n^3) \\ &= {\frac{3}{4}}n^5 + {\frac{1}{4}}n^3 , \\ S_{n-1}^{\,\,3} - S_{n-2}^{\,\,3} & = {\frac{3}{4}}{(n-1)}^5 + {\frac{1}{4}}{(n-1)}^3 ,\\ S_{n-2}^{\,\,3} - S_{n-3}^{\,\,3} & = {\frac{3}{4}}{(n-2)}^5 + {\frac{1}{4}}{(n-2)}^3 , \\ \\ \\ \dots\dots\dots & \dots\dots\dots\dots\dots ,\\ \\ S_2^{\,3} - S_{1}^{\,3} & = {\frac{3}{4}}2^5 + {\frac{1}{4}}2^3 , \\ S_1^{\,3} - S_{0}^{\,3} & = {\frac{3}{4}}1^5 + {\frac{1}{4}}1^3 .\end{align}

When we add these equations, we obtain: \[ {S_n^{\,3}} = {\frac{3}{4}}\Big(1^5 + 2^5 + 3^5 + \cdots + n^5\Big) + {\frac{1}{4}}\Big(1^3 + 2^3 + 3^3 + \cdots + n^3\Big) ,\] or \[ {{(1+2+3+\cdots +n)}^3} = {\frac{3}{4}}\Big({1^5 + 2^5 + 3^5 + \cdots + n^5}\Big) \] \[ + {\frac{1}{4}}\Big({1^3 + 2^3 + 3^3 + \cdots + n^3}\Big) ,\] as can be seen in Figure 7.

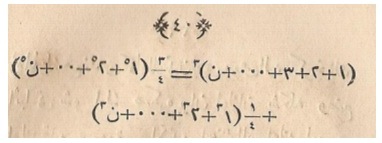
Figure 7. An equation involving the sum of the fifth powers (from Mebahis-i İlmiyye, 1867, courtesy of the authors).

We already know that \[ 1^3 + 2^3 + 3^3 + \cdots + n^3 = {{(1+2+3+\cdots +n)}^2} = {\bigg[ {\frac{n(n+1)}{2}}\bigg]}^2 \] and \[{1 + 2 + 3 + \cdots + n} = {\frac{n(n+1)}{2}}.\] When we substitute these identities into the equation in (or just above) Figure 7, we obtain: \[ {\bigg[ {\frac{n(n+1)}{2}}\bigg]}^3 = {\frac{3}{4}}\Big(1^5 + 2^5 + 3^5 + \cdots + n^5\Big) + {\frac{1}{4}}{\bigg[ {\frac{n(n+1)}{2}}\bigg]}^2 . \]

If we then re-arrange this equation, we can find a formula for the sum of the fifth powers: \[ {1^5 + 2^5 + 3^5 + \cdots + n^5} = {\frac{4}{3}}\Bigg({{\bigg[ {\frac{n(n+1)}{2}}\bigg]}^3 - {\frac{1}{4}}{\bigg[ {\frac{n(n+1)}{2}}\bigg]}^2}\Bigg) \] or \[ {1^5 + 2^5 + 3^5 + \cdots + n^5} = {\frac{1}{6}}n^6 + {\frac{1}{2}}n^5 + {\frac{5}{12}}n^4 - {\frac{1}{12}}n^2 . \]