- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
El Gabinete de Maravillas Matemáticas de Pantas: Imágenes e Historia de las Matemáticas – Selección de Imágenes – Artefactos Antiguos
Las búsquedas informáticas apropiadas revelan una gran cantidad de imágenes de instrumentos para medir y hacer cómputos; de personas que contribuyeron a las matemáticas; y de trabajos matemáticos existentes, como libros y notas, que pueden usarse para enriquecer la enseñanza y el aprendizaje de las matemáticas [Kidwell 2021]. Si se conocen por su nombre, se pueden buscar; por ejemplo, imágenes del hueso de conteo de Ishango, el artefacto matemático humano más antiguo que existe, ya que están disponibles en internet, incluyendo un “tesoro matemático” aquí en MAA Convergence. (Ver Figura 5.)

Figura 5. Se cree que el hueso de conteo de Ishango tiene entre 20.000 y 25.000 años de antigüedad. (Imagen cortesía del Museum of Natural Sciences, Bruselas, Bélgica. Se puede usar esta imagen en la sala de clases; todos las demás imagenes requieren permiso del Museum of Natural Sciences, Royal Belgian Institute of Natural Sciences.)
La edad del hueso de Ishango, 20.000–25.000 años, es testigo de la larga conexión humana con las matemáticas y la necesidad de registrar datos matemáticos. Las conjeturas sobre su función preparan a la audiencia para una discusión de la numeración en general. Esto puede llevar al tema de los palos de conteo, y la historia bastante interesante y divertida del incendio de la Oficina del Tesoro Británico de 1826. Debido a la eliminación por quema en la oficina de palos de conteo acumulados por siglos, la Cámara de los Lores fue incendiada y quemada.
Una imagen muy efectiva y cargada de información que ha aparecido en varios libros sobre la historia de las matemáticas es Yale Babylonian Cuneiform 7289 (YBC 7289), una tablilla cuneiforme del período babilónico antiguo (circa 1900–1600 aC). (Ver Figura 6.)
 |
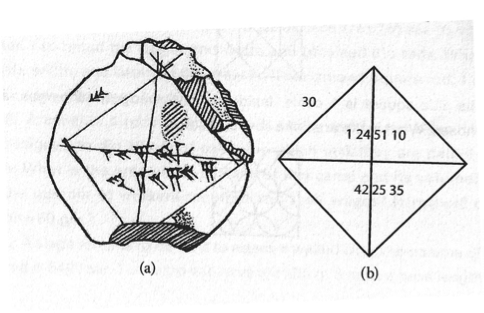 |
Figura 6. La "tablilla de palma" de arcilla que se muestra arriba, a la izquierda, cabría en la mano de un antiguo escriba mesopotámico. Una transcripción y traducción se muestran a la derecha. (Imagen de la izquierda cortesía de la Colección Babilónica de Yale. Se puede usar esta imagen en el salón de clases; todas las demás imagenes requieren permiso de la Colección Babilónica de Yale. Las imágenes de la derecha aparecen en la página 27 del libro de Asger Aaboe [1998, originalmente escrito en 1964] y se reproducen aquí por cortesía de la Mathematical Association of America.)
Primero, se observa el tamaño físico de la tableta de arcilla. Cabe en la mano de un hombre, y de hecho era una tableta de palma, sostenida convenientemente en la palma de una mano mientras el escriba, usando su otra mano, escribía en ella. Los estudiantes modernos visualizan las mesas de arcilla cuneiformes como bastante grandes, tal vez están influenciadas por las ilustraciones bíblicas estilizadas de Moisés sosteniendo las tablas de los Diez Mandamientos judeocristianos. Pero la característica más llamativa para el espectador novato es que el diagrama muestra claramente un cuadrado con sus diagonales. Sí, los antiguos babilonios dibujaron diagramas geométricos exactos en arcilla como parte de sus discusiones matemáticas. Una vez, cuando ofrecí esta ilustración en un artículo para su publicación, fui desafiado por el editor de la revista, quien sospechaba que yo mismo había dibujado el diagrama y estaba atribuyendo falsamente sus orígenes a los babilonios. Incluso las personas muy sofisticadas no aprecian el hecho de que los matemáticos antiguos dibujaron diagramas geométricos para ayudar en la resolución de problemas.
A continuación, un desciframiento de la inscripción cuneiforme revela dos números en notación sexagesimal: lo que conocemos como \(\sqrt 2\) y \(\sqrt 2\times 30,\) donde \(30\) es la longitud especificada del lado del cuadrado. (Ver Figura 6b.) En este punto de la inspección, surgen dos implicaciones:
- que en este período temprano antes del ascenso de Grecia y los pitagóricos, los babilonios poseían lo que generalmente conocemos como “el Teorema de Pitágoras”, y
- que estos pueblos antiguos podían extraer la raíz cuadrada de un número, con varios decimales de precisión.
Entonces surge otra pregunta obvia: “¿Cómo lo hicieron?” Además, si uno mira de cerca la imagen, ¡puede ver la huella digital humana “reveladora”!
Además del libro de Aaboe, las imágenes y la discusión de esta tableta aparecen en libros de texto, incluídos Burton [1997, p. 77] y Hodgkin [2005, p. 25].
Frank J. Swetz (The Pennsylvania State University), "El Gabinete de Maravillas Matemáticas de Pantas: Imágenes e Historia de las Matemáticas – Selección de Imágenes – Artefactos Antiguos," Convergence (August 2022)




