Mathematical Treasure: Works by Abraham de Graaf

Abraham de Graaf (1635–1717) was a mathematician, publisher, reckoning master, bookseller, and linen weaver in Amsterdam. As an enterprising reckoning master, he taught a broad range of mathematical topics and the applications of mathematics including accounting, mechanics and navigation. He was also a prolific author. We shall examine here several of his mathematics works that can be accessed via the HathiTrust in some cases and the Making of the Modern World database in others.

1. Instructie van het Italiaans boekhouden : met een memoriaal toepast op de negotie particulier, in commissie en in compagnie was first published in 1688 and would eventually go on to realize 50 editions. This was the most popular of de Graaf’s publications. It introduced the Italian method of accounting to the merchants and tradesmen of Amsterdam.

2. Principia arithmeticae, theoreticae, & practicae: of De beginselen der telkunst, of rekenkunst; …, 1662, was a basic arithmetic book. Readers will acquire skills in rekenkunst, mathematics.

Some sample pages from this text:

3. De beginselen van de algebra of stelkonst, volgens de manier van Renatus Des Cartes verklaart met uytgelezene voorbeelden ; …, 1672, was built upon René Descartes’ work.

4. De geheele mathesis of wiskunst, herstelt in zijn natuurlijke gedaante, first published in 1676 and shown here in a 1694 printing, was a discussion of the applications of mathematics.

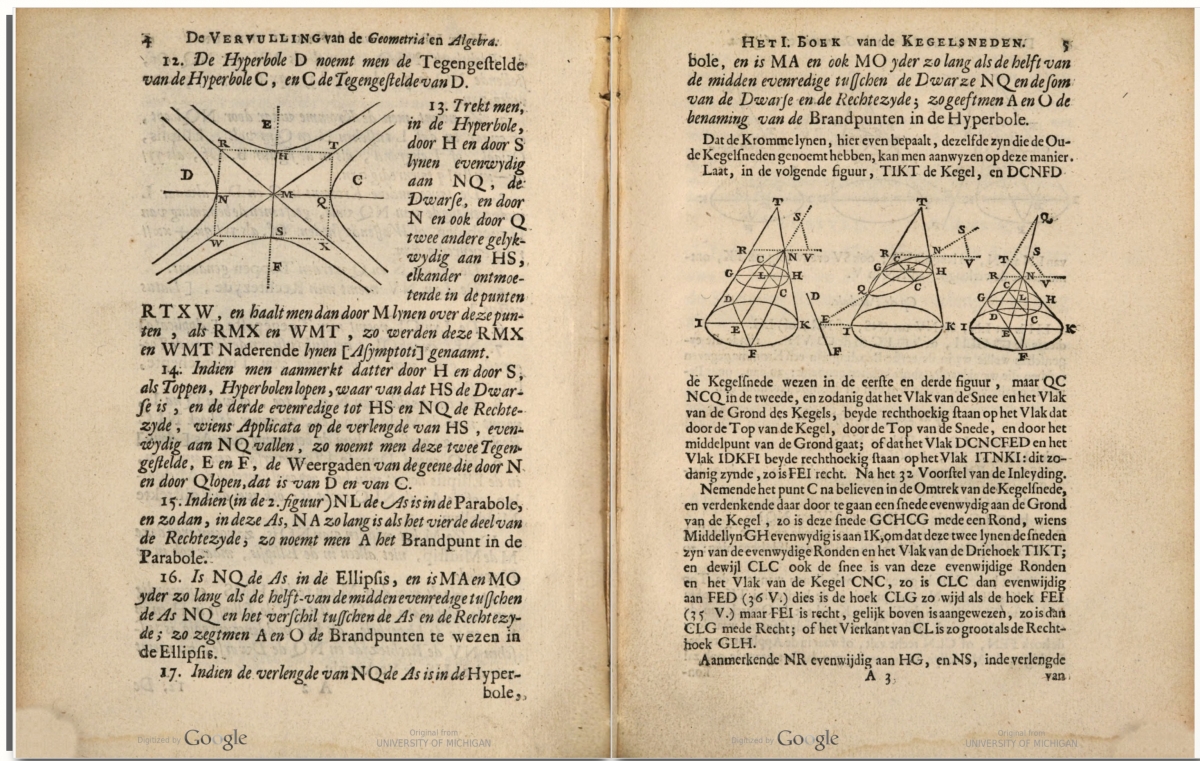
5. De vervulling van de geometria en algebra, begrepen in het boek genaamt de Inleyding tot de wiskunst: handelende van de voornaamste eygenschappen der kegelsneden, en de ontbinding der aequatien van drie, vier, en meer dimensien tot in't oneyndig, 1708, is what the modern reader would recognize as analytic geometry. Eventually, 30 printings of this work would be published. In it, de Graaf defines the conic sections. He then illustrates just how they can be constructed using a variety of instruments. Finally, he algebraically examines the curves, noting their mathematical properties.

Some sample pages from this text. Note the use of Descartes’ equal sign in the algebraic equations:

6. Exemplaar-boekje van de arithmetica, zynde een vervolg van de Wiskonstige arithmetica, originally published in 1702, went on in seven editions up to 1758. Later editions were revised by other mathematicians. This book provides a brief introduction to basic arithmetic and then presents a series of problems. These problems focus on the commercial concerns of Amsterdam’s business community.

7. Analysis of stelkunstige ontknoping in de meetkunstige werkstukken : vindende van hen de grootste en kleenste ; de raaklynen op de kromme ; de plaatzen ; de ontbinding der bepaalde werkstukken door de plaatsen ; en de quadratura van eenige kromlinische grootheden, an introduction to calculus. The book was published in 1706 and went through seven other editions in the same year. 

8. Inleyding tot de wiskunst, of de beginselen van de geometria en algebra experienced 6 editions after being first published in 1706 in Dutch. In this book, de Graaf demonstrated the use of algebra to describe geometric curves.

Index to Mathematical Treasures