- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Approximate Construction of Regular Polygons: Two Renaissance Artists - Leonardo da Vinci
Leonardo da Vinci (1452-1519) was many things: painter, physicist, engineer, anatomist... and amateur mathematician. He was not a methodic writer, but now and then he would note down a construction procedure for some regular polygon. (Some of them he later considered bad enough to label them “falso”.)
We will review here his construction of the regular pentagon . (It is approximate; an exact one was given by Euclid.)
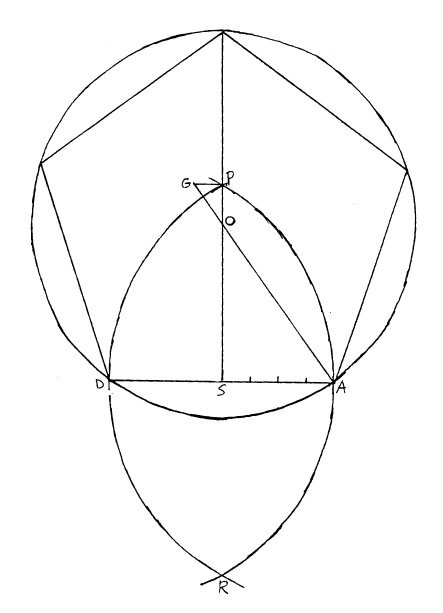
Let the given side of the regular pentagon be DA=a. Drawing circles of radius a, centered at D and at A, we obtain points P and R on the perpendicular bisector of DA. We then divide DA into eight equal parts. We now draw PG ||AD, with PG = AD/8; AG and PS intersect at O, center of the circle circumscribed about the sought pentagon. From here, we can proceed easily: it is only necessary to copy angle AOD = 2p/5 four more times.
How accurate is this procedure? To find out, we need only note that since triangles SAO and PGO are similar, it follows that AS/PG = SO/OP = 4/1. And since triangle DAP is equilateral of side a, SP, the altitude of this triangle, has length a √3/2. Then, the tangent of angle SOA is equal to the tangent of angle GOP. This tangent is easily calculated to be
PG/OP = ( a/8)/(a√3/10) = (5/12)√3.
Therefore, the sine of angle SOA is (5/73)√73 = 0.585.
This is, in fact, a good approximation, as it makes sin 36° = 0.585 instead of 0.587. [1] Of course, 36° = (1/2)(360°/5).
Raul A. Simon, "Approximate Construction of Regular Polygons: Two Renaissance Artists - Leonardo da Vinci," Convergence (August 2010)




