Mathematics as the Science of Patterns - Euclid (continued)

Let circle ABCD be given and let chords AC and BD meet at E (see fig. 2).   We need to show that the rect.DE,EB equals rect.AE,EC.  From the center Z, draw ZH and ZQ perpendicular to AC and BD (thus, also, H bisects AC and Q bisects BD), respectively, and let ZE, ZB, and ZC be joined.     

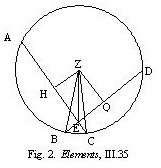
Thus, by the theorem quoted from Book II, rect.AE,EC together with sq.HE equals sq.HC. Therefore, also, rect.AE,EC together with sq.HE and sq.ZH equals sq.HC and sq.ZH.  But, sq.HE and sq.ZH equals sq.ZE, while sq.HC and sq.ZH equals sq.ZC, by the ‘Pythagorean Theorem’ (proposition 47 in Book I of the Elements).  So, rect.AE,EC together with sq.ZE equals sq.ZC.  Similarly, rect.DE,EB together with sq.ZE equals sq.ZB.  But, ZC is equal to ZB because they are radii.  Therefore  rect.AE,EC together with sq.ZE equals rect.DE,EB together with sq.ZE, so that, rect.AE,EC equals rect.DE,EB.

Geometry lessons usually include also the complement to propositions 35 and 36, namely, that if two lines from a point outside a circle cut the circle then the rectangle contained by the whole of one of the lines and its exterior segment is equal to the rectangle contained by the whole of the other line and its exterior segment (call it 36*).  This proposition, however, is not found in the Elements.  The reason, presumably, is simply that the proposition follows from proposition 36 almost immediately; Euclid does not have to spell out explicitly every property of circles that can be easily deduced from the main propositions. 

But is this not the important point?  Euclid is interested in finding properties of geometrical objects, not patterns they manifest.  A pattern in propositions 35, 36, 36* emerges particularly clearly when one gets over what Descartes’ called the “scruple that kept the ancients from using arithmetical terms in geometry” (La Géométrie , p.305) and writes these propositions, as we do now and Euclid did not do, in terms of products.  Thus, if AC and BD are chords of a circle meeting at a point E (see fig. 3), it will always be the case that AExEC=BExED, even where B and D are the same (i.e. when EB is tangent to the circle). 

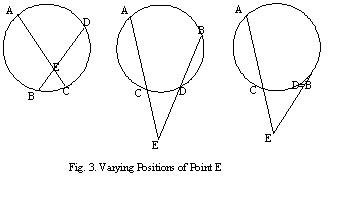
One with an algebraic eye can spot a slightly different, and even more compelling, pattern in Euclid’s own proof.  It is where, in the course of the proof, Euclid shows that rect.AE,EC together with sq.ZE equals sq.ZC (see fig. 2): let ZE, which is the distance between the center of the circle and the point E where the chords meet, be d, and let ZC, which is the radius of the circle, be r.  Then, AExEC + d²= r² or AExEC = r²- d².  Similarly, had we gone over the proof for proposition 36* where E is outside the circle, we would have found that AExEC + r²= d² or.  Thus, AExEC = r²- d²   if E is inside the circle, AExEC= d²- r²   if E is outside the circle, and, obviously, AE x EC=0 if E is on the circle (for then d=r).  Put even more succinctly, if AC is any chord of a circle through a point E (possibly on the circumference of the circle so that C and E or A and E coincide), then AE x EC=|r²-d²|.  This brings us to Jacob Steiner.