Mathematical Treasure: L’Hospital’s Analyse des Infiniment Petits

Billed as the first differential calculus textbook, Analyse des Infiniment Petits, Pour l’intelligence des lignes courbes (Analysis of the infinitely small to understand curved lines), was written by Guillaume François Marquis de l’Hospital. The first edition of this French book was published in 1696, with other editions appearing posthumously from 1716 to 1781. The book is credited with introducing many French mathematicians and others to the differential calculus of Leibniz. In the preface, l'Hôpital mentions that he focuses on just differential calculus since Leibniz was writing a book (which was never finished) on integral calculus. L'Hôpital also credits Johann Bernoulli, whom he had hired to teach him the calculus of Leibniz. In fact, there is some question as to how much of the material in the Analyse is due to l'Hôpital and how much to Johann Bernoulli. Below is a portrait of the author from the frontispiece of the first edition. Notice his last name is spelled as l’Hospital, although today it is more often seen in a modernized form, l'Hôpital.

Next is a copy of the title page.

The images below show the two pages of the Table of Contents of the Analyse.  Notice the title of Chapter 1 which translates as In which we give the Rules of the calculus of Differentials.

Below, the first page of the text begins with definitions of variable and constant.

Here on page 5 is Proposition III, the quotient rule.

While on page 15, we see an example of drawing a tangent line to y³ – x³ = axy with the accompanying figure.

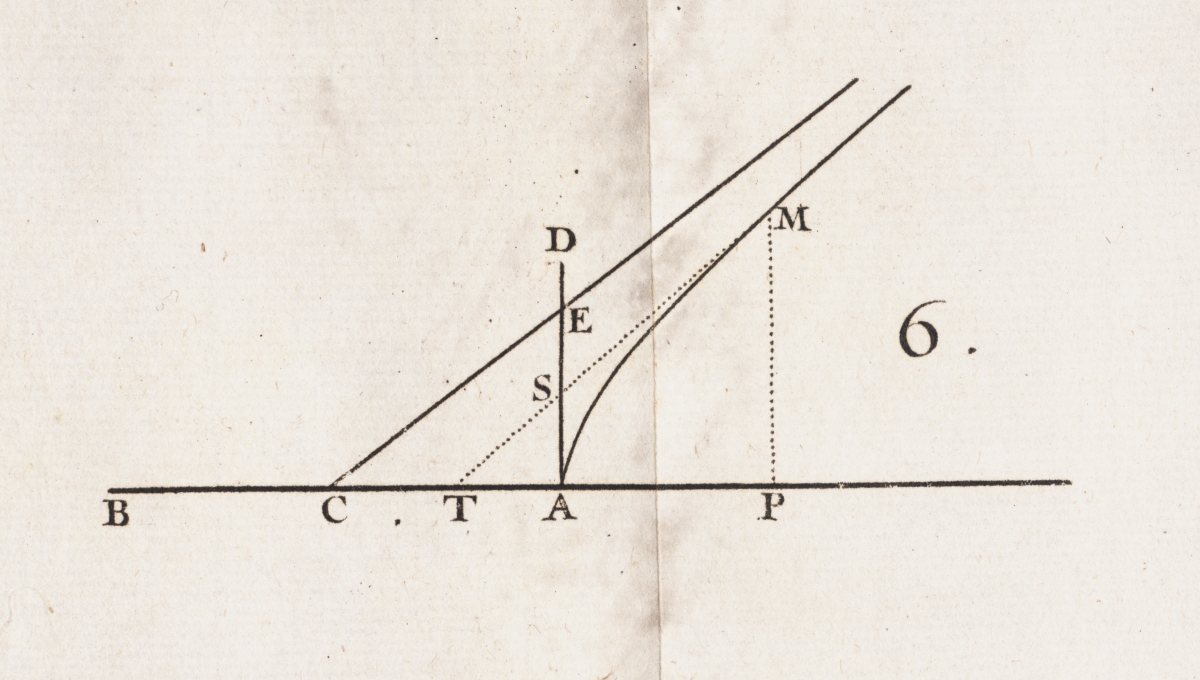
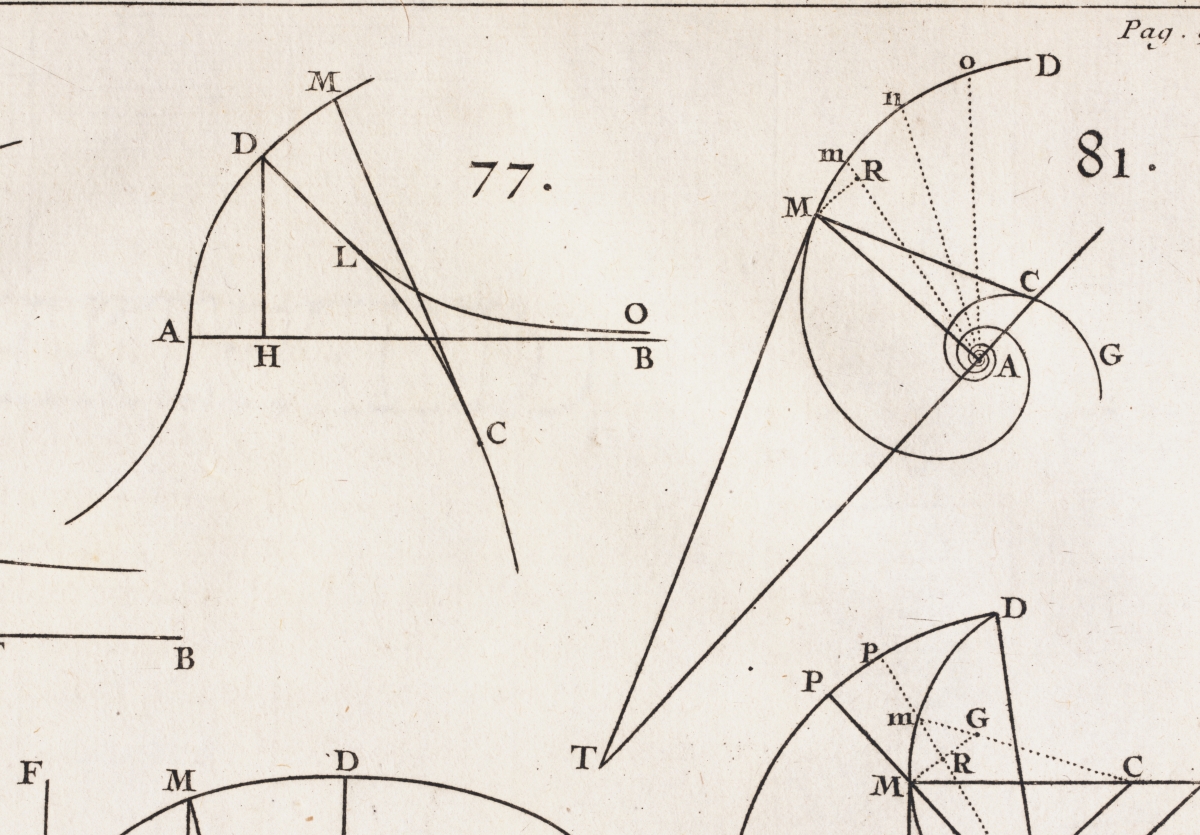
Below are two more pages from the Analyse. Page 55 is the start on the section about inflection points and page 89 looks at the logarithmic spiral.

The discussion of what is now known as l’Hôpital’s rule is found on pages 145–147.

Images from another copy of the 1696 edition of l’Hôpital’s Analyse can also be found in Convergence.

An English translation with commentary was published in 2015.

A complete digital scan of the Analyse is available in the Linda Hall Library Digital Collections. The call number is QA302 .L49 1696.

Images in this article are courtesy of the Linda Hall Library of Science, Engineering & Technology and used with permission. The Linda Hall Library makes available all existing digital images from its collection that are in the public domain to be used for any purpose under the terms of a Creative Commons License CC by 4.0. The Library’s preferred credit line for all use is: “Courtesy of The Linda Hall Library of Science, Engineering & Technology.”

References

Boyer, Carl. The History of the Calculus and Its Conceptual Development. Dover, 1949, pp. 238, 241.

Bradley, Robert E., Salvatore J. Petrilli, and C. Edward Sandifer. L’Hôpital's Analyse des infiniments petits, An Annotated Translation with Source Material by Johann Bernoulli. Birkhäuser, 2015.

Underwood, Edward Dudley (Ed.). Readings for Calculus, Volume 5 of Resources for Calculus, MAA Notes Volume 31. The Mathematical Association of America, 1993, pp. 60–63.

Index to Mathematical Treasures