- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasure: John Lodge Cowley’s Solid Geometry
John Lodge Cowley, An illustration and mensuration of solid geometry; in seven books: containing forty-two moveable copper-plate schemes for forming the various kinds of solids, and their sections; by which the doctrine of solids in general, and those in the eleventh, twelfth, and fifteenth books of Euclid are elucidated, and rendered more easy to learners than by any other work hitherto published, 3rd ed. (London, 1787).
Introduction
During our honeymoon in Europe in the summer of 1971, my wife (also a math major) bought me a wedding gift from Bernard Quartich Ltd. Rare Books in London: the 1787 third edition of Cowley’s solid geometry book. Having launched my teaching career the year before, I was fascinated by such an early use of hands-on fold-up figures to aid in the teaching of three-dimensional geometry. Moreover, I deeply appreciated the beauty of the small folio tree calf binding and the expert engravings that produced the forty-two moveable models, which looked stunning when folded up. Owning the book motivated me to decorate my first classroom with hanging models of the Archimedean and Platonic Solids, to develop hands-on lessons for my junior high school Algebra students to discover Euler’s formula, and to give my Geometry students a proof of why there are only 5 Platonic Solids.
About John Lodge Cowley
John Cowley (1719-1797) was a recognized mathematician in 18th-century England. He became professor of mathematics at the Royal Military Academy, Woolwich, in 1761 and remained there until 1773; Charles Hutton also taught at the academy. He was elected a Fellow of the prestigious Royal Society in April 1768. He was also an important geographer as well as Cartographer Royal to King George II. Cowley produced maps that depicted the counties of England, resulting in his most famous work, Counties of England. He published several other maps in remarkable detail with his name and the name of the engraver on them. Another of his publications was A new and easy introduction to the study of geography; it was structured as questions and answers with decorative maps added later. His maps contained longer titles than those usually found on the standard miniature maps. He also published a number of introductory works on solid geometry with fold-up figures to aid learners: Geometry Made Easy (1752), An Appendix to Euclid’s Elements (1758) and The Theory of Perspective Demonstrated (1765).
Cowley taught geometry to subscribers of the St. Martin's Lane Academy, a drawing school established by the eminent artists William Hogarth and John Ellys. Such work supplemented his income from the Royal Military Academy. Cowley died in Walworth, Surrey, in 1797. His daughter inherited his passion for science, instructing many members of the British nobility in the use of globes and maps.
An illustration and mensuration of solid geometry (1758) anticipates the work of future authors such as Oliver Byrne, who nearly 100 years later, sought to provide a highly visual way to study Euclid using color.
The Book

Title page, from the collection of Dr. Sid Kolpas.

Tree calf binding of the author’s 1787 third edition. Tree calf is a highly polished calf binding that originated in the late 18th century in which the leather was stained to produce a dark tree-like pattern on the front and rear boards.
The author’s copy is the 1787 small folio third edition, revised, corrected, and augmented by William Jones. It was meant to be a treatise for the use of workmen, and is considered useful for students in the field of perspective drawing. Obviously, it can also be used to teach concepts and mensuration in solid geometry. The book was constructed so that, by means of the fold-up models, one can study the forms of the three dimensional solids and meaningfully do mensuration on them. The first edition was published in 1758, and the second in 1765. The English Short-Title Catalog (ESTC) database lists only 6 copies of the first edition housed in libraries around the world. As noted above, Cowley’s work presages the work of Oliver Byrne, almost 100 years later, of using visual methods to teach Geometry.

Tetrahedron folded up.

Cube or Hexahedron folded up.

Unfolded Dodecahedron.

Unfolded Solid Rhombus.

Partially folded Dodecahedron inscribed in an Icosahedron.
Use in the Classroom
Cowley’s work can be used in Mathematics Education classes to discuss kinesthetic activities for teaching geometric concepts. It can also serve as motivation for lessons and projects in Geometry classes. Students can make models, for example, of the Platonic Solids, and discover Euler’s Formula (V - E + F = 2) while reviewing Vertices, Edges, and Faces.
Students may also enjoy a proof of why there are only 5 regular (Platonic) solids. This proof reviews regular polygons and the fact that each angle in a regular polygon has (n - 2)180/n degrees when n is the number of sides; therefore each interior angle of an equilateral triangle is 60 degrees, each interior angle of a square is 90 degrees, each interior angle of a regular pentagon is 108 degrees, and each interior angle of a regular hexagon is 120 degrees. We first search for two-dimensional diagrams consisting only of equilateral triangles. A minimum of 3 such triangles converging at the same vertex are needed to fold up to a 3-dimensional shape. So, it would require either 3 equilateral triangles at a vertex (adding to 180 degrees) or 4 equilateral triangles at a vertex (adding to 240 degrees) or 5 equilateral triangles at a vertex (adding to 300 degrees). There could not be 6 equilateral triangles at a vertex because that adds to 360 degrees, and it would not be possible to fold up the diagram into a 3-dimensional shape.
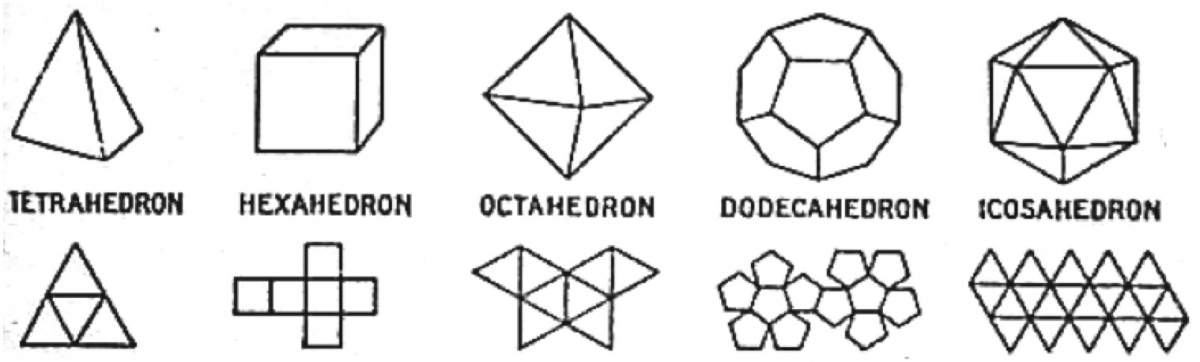
Those valid choices give us the patterns for the tetrahedron (3 equilateral triangles at a vertex), octahedron (4 equilateral triangles at a vertex), and icosahedron (5 equilateral triangles at a vertex).
Next, we investigate patterns with squares. A minimum of 3 converging at the same vertex are needed to fold up to a 3-dimensional shape. So, it would require either 3 squares at a vertex (adding to 270 degrees) or 4 squares at a vertex which adds to 360 degrees, in which case the folder would not be able to fold up the diagram into a 3-dimensional shape. So, the only pattern is that of a hexahedron, or cube, with 3 squares converging at the same vertex.
Next, classes can investigate patterns with regular pentagons. A minimum of 3 converging at the same vertex are needed to fold up to a 3-dimensional shape. So, it would require either 3 regular pentagons at a vertex (adding to 324 degrees) or 4 regular pentagons at a vertex which adds to 432 degrees, in which case one could not fold up the diagram into a 3-dimensional shape. So, the only pattern is that of a dodecahedron with 3 regular pentagons converging at the same vertex.
Next, we investigate patterns with regular hexagons. A minimum of 3 converging at the same vertex are needed to fold up to a 3-dimensional shape. So, it would require 3 at a vertex (adding to 360 degrees), but one would not be able to fold up the diagram into a 3-dimensional shape. Our search is done. There are only 5 regular polyhedra.
In a History of Mathematics class, Cowley's book could motivate a discussion of Plato, his mathematical contributions (such as Socrates and the Slave Boy), and what he thought the Platonic Solids represented. One could also discuss Kepler and how he used the Platonic Solids to investigate the solar system.
Also in Convergence
See fold-up figures in the 1570 Elements of Geometrie of ... Euclide ..., the first publication of Euclid's Elements in English, in the Convergence Mathematical Treasure, "Billingsley's Euclid."
The Convergence article "Leonardo Da Vinci's Geometric Sketches" includes images of the Platonic solids, created for Luca Pacioli's De divina proportione (1509).
For images of Oliver Byrne's colorful 1847 edition of Euclid's Elements, see the Mathematical Treasure, "Oliver Byrne's Euclid," and the article "Oliver Byrne: The Matisse of Mathematics," by Susan Hawes and Sid Kolpas.
Index to Mathematical Treasures
References
Astley Book Farm. http://www.astleybookfarm.com/.
Taylor, E. G. R. The Mathematical Practitioners of Hanoverian England, 1714-1840. Cambridge University, 1966.
"John Lodge Cowley." Wikipedia. https://en.wikipedia.org/wiki/John_Lodge_Cowley.
Sidney J. Kolpas (Delaware County Community College), "Mathematical Treasure: John Lodge Cowley’s Solid Geometry," Convergence (March 2017)




