- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasure: 13th Century Islamic Geometry Treatise
Abū ʻUthmān al-Shaykh al-Ṭajibī (or al-Ṭujībī) was a renowned surgeon in 13th century Islamic Spain. Obviously, he also had an interest in geometry as he composed a brief treatise on geometry in which he considered the properties of triangles, quadrilaterals and circles. In fact, the word “al-Shaykh” in his name is an honorific for a scholar, a master of a subject. Here are four folios from this brief treatise.

On page 6 above is a discussion of the various types of triangles. At one time, the page margin contained several illustrations that have faded over time. The page numbers are written in the ghubār (“dust”) system of digits that arose in the western Arab world in the Middle Ages, and which was the most direct ancestor of the modern Western set of digits.
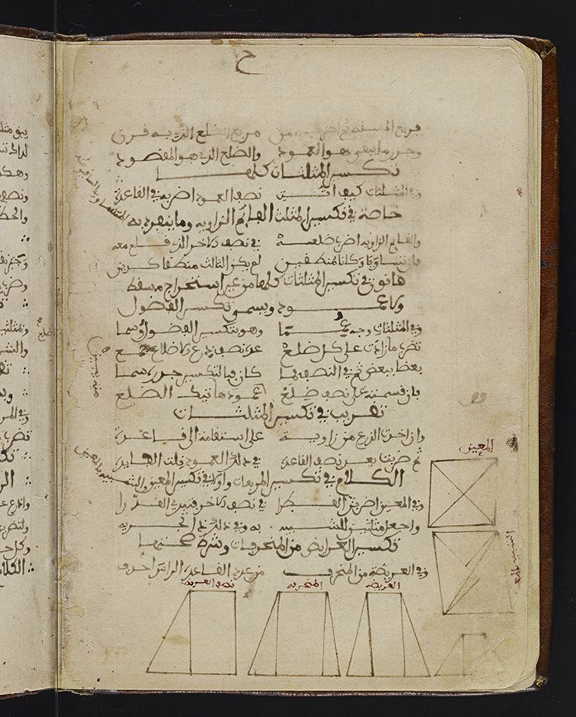
On page 7 above, methods are introduced for calculating the areas of trapezoids and parallelograms by dissecting them into triangles and rectangles.

The circle is discussed here on the page above. Several marginal diagrams have faded due to age.

From the fragments of drawings remaining in its left margin, one can see that this folio considers circular segments, lunes, inscribed circles, and regular polygons.
The images above were obtained from the Digital Collection of the University of Pennsylvania (Lawrence J. Schoenberg Collection). The complete work is available for viewing via its reference number, LJS 465.
Acknowledgment
We thank Randy K. Schwartz of Schoolcraft College for his contributions to this article.
Frank J. Swetz (The Pennsylvania State University), "Mathematical Treasure: 13th Century Islamic Geometry Treatise," Convergence (January 2016)




