Jan Hudde’s Second Letter: On Maxima and Minima - Mathematical Background: Double Roots

Building on the work of Fermat and Descartes [Curtin, pp. 263-264], Hudde considered algebraic expressions set equal to \(z\) and sought the maximum value for \(z.\) Strictly speaking his procedure finds a local maximum, but I will say “maximum” as he does. I will also use functional notation in this section, though Hudde did not.

In our notation Hudde wanted to find the maximum value \(z_{\rm{max}}\) of \(f(x) = z.\) This will occur when \(f(x) = z\) has a double root. For smaller values of \(z,\) \(f(x) = z\) will have two (or more) solutions (see Figure 1).

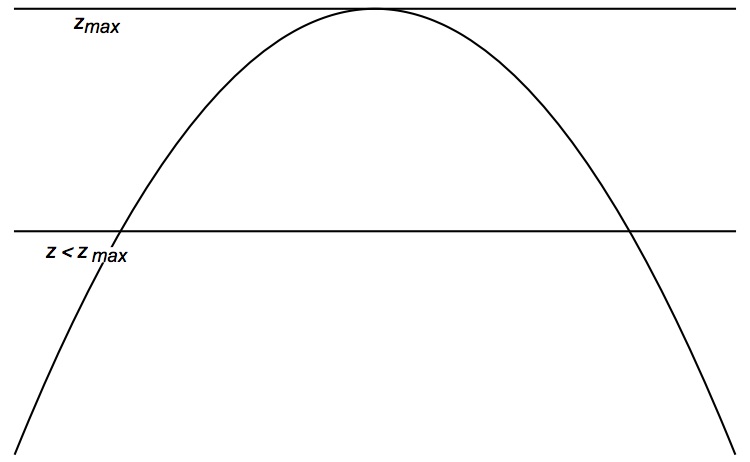
Figure 1. Near its maximum value, \(f(x) = z\) has two (or more) solutions; at the maximum value \(z_{\rm{max}},\) \(f(x) = z\) has a double root.

For a minimum, invert the picture. Hudde recognized that the procedure for finding maxima and minima was the same. His theorem statements refer to both, though his examples use only the word “maximum.”

Double Roots

For algebraic functions the problem of finding a double root is purely algebraic. No limit or infinitesimal quantity is needed.

Hudde’s letter begins with a theorem telling how to do this [Hudde, p. 507]. For a polynomial

\[p(x) = c_0 + c_1x + c_2x^2 + \cdots + c_nx^n\]

and any arithmetic progression \(a, a+b, a+2b, a+3b,\dots,\) combine the two to get

\[{\hat p}(x) = ac_0 + (a+b)c_1x + (a+2b)c_2x^2 + \cdots + (a+nb)c_nx^n.\quad (1)\] In our notation, we can see

\[{\hat p}(x) = ap(x)+bxp^{\prime}(x).\quad\quad\quad\quad\quad\quad (2)\]

Hudde claimed that if \(p(x) = 0\) has a double root at \(x=x_0,\) then \({\hat p}(x) = 0\) has a single root there. The converse, which is what Hudde really needed, is also true, though Hudde left this implicit.

To prove this, we might proceed as follows. Assume \(p(x) = 0\) has a double root \(x=x_0.\) Thus \(p(x) = {{(x-{x_0})}^2}{q(x)},\) where \(q(x)\) is a polynomial that is not zero at \(x_0.\) From (2),

\[{\hat p}(x) = a{{(x-{x_0})}^2}q(x) + bx[2(x-{x_0})q(x) + {{(x-{x_0})}^2}{q^{\prime}(x)}] \]

\[=(x-{x_0})[ a{(x-{x_0})}q(x) + 2bxq(x) + {(x-{x_0})}{q^{\prime}(x)}].\]

Since \(q(x_0)\not=0,\) the quantity in the square brackets will not be zero, unless \(x_0 = 0,\) in which case identifying a double root would be quite easy.

How did Hudde argue? He looked at the simplest example with a double root, namely \(x=y\):

\[p(x)=x^2-2xy+y^2={(x-y)}^2=0.\]

Apply the progression to obtain

\[{\hat p}(x) = (a+2b)x^2-2(a+b)xy+ay^2=0.\]

Hudde considered it obvious that \(y\) is a single root. We might elaborate

\[0=(a+2b)x^2-2(a+b)xy+ay^2=a{(x-y})^2+2b(x^2-xy)\]

\[=(x-y)[a(x-y)+2bx],\]

and this expression has \(y\) as a single root (again excepting the easy case \(y=0\)).

For the general case, Hudde gave an example that easily generalizes. He considered the following equation, which has \(y\) as a double root:

\[{(x-y)}^2(x^3+px^2+qx+r)=0.\]

Expanding the quadratic,

\[(x^2-2xy+y^2)x^3+p(x^2-2xy+y^2)x^2+q(x^2-2xy+y^2)x+r(x^2-2xy+y^2)=0.\]

If the left-hand side is expanded into powers of \(x\) and each term \(x^k\) multiplied by the corresponding term \(a+kb\) of an arithmetic progression, \(k=0,1,2,3,4,5,\) then each of the occurrences of \( x^2-2xy+y^2\) is multiplied by a different progression. For example,

\[(x^2-2xy+y^2)x^3=x^5-2x^4y+x^3y^2\]

becomes

\[[(a+5b)x^2-(a+4b)2xy+(a+3b)y^2]x^3.\]

Thus \(y\) is a single root of this piece, by the argument for \(x^2-2xy+y^2=0\) and any arithmetic progression. Since this works for each piece, it follows that \(y\) is a single root of the entire equation.

Clearly, if the cubic factor is replaced by any polynomial or rational expression (that isn’t \(0\) at \(y\)), the same argument applies. Hudde also observed that if the expression starts with a triple root, then the transformed expression has a double root, etc.