Reflections on Chinese Numeration Systems: Advanced Applications

The oldest extant Chinese mathematical classic, the Jiuzhang Suanshu (Nine Chapters on the Mathematical Art) of ca 200 BCE, provides evidence of varied, and more advanced, Chinese mathematical activity [Schwartz 2018]. For example, the division process using rods was modified and developed into a strategy for extracting square and cube root of numerical quantities. Before the first year of the Christian calendar, Chinese mathematicians were obtaining accurate numerical roots to three decimal places. Their technique would appear much later in European mathematical history, in 1819, described as “Horner’s Rule” and named after the British mathematician William George Horner (1786–1837).

The contents of the Jiuzhang also indicate that Chinese users were familiar with the binomial expansion as well as posing and solving quadratic and cubic equations. A systematic means for determining the numerical coefficients of the binomial expansion was devised by mathematician Jia Xian around 1100 CE. Jia depicted the coefficients in a triangular array. Later, the noted mathematician Yang Hui (fl. 1238–1298) expanded Jia’s work and published his findings in an enlarged triangular figure. Within this diagram, Yang expressed his numbers using rod numerals. Six hundred years hence, this numerical triangle would become known as “Pascal’s Triangle,” honoring the French mathematician Blaise Pascal (1623–1662).

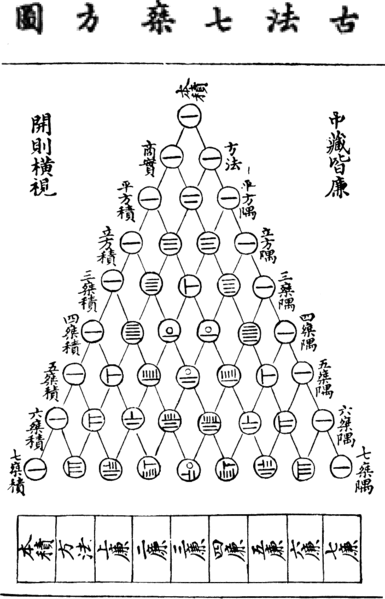
Figure 8. Wood cut print of Yang’s triangle as published in 1303 by the mathematician Zhu Shije in his Si Yuan Yu Jian. Can you read the numbers? (Some are variant versions.) Is there a mistake? Wikimedia Commons.

The peak of Chinese algebraic accomplishment using computing rods and a board was achieved in the 14th century by the mathematician Zhu Shijie (c. 1260–c. 1320). Zhu developed a method to solve equations containing up to four unknowns. His “Four Element Method,” as discussed in his Si-yüan yü-jian (Jade Mirror of the Four Unknowns) of 1303 CE, included the entities known as: Heaven, Earth, man, and matter.

Rod layouts on the computing surface also revealed visual numerical patterns that mathematicians could interpret. Rectangular arrangements were most common. In working out problems with rods, Chinese mathematicians recognized the existence and influence of unknown variables. They distinguished between them and allowed for their presence within rod configurations. Systems of linear equations could be laid out as rectangular arrays of rods. For instance, the eighth chapter of the Jiuzhang Suanshu discussed such systems. In contemporary mathematics, we would recognize such an array as a matrix [Hart 2011]. The ancient Chinese calculators treated them as such and solved them by matrix-like operations that today we would recognize as Gaussian Elimination, a process credited to the German mathematician Carl Friedrich Gauss (1777–1855) [Grcar 2011]. Chinese solution techniques also allowed for the consideration of linear systems involving indeterminant situations.