John Napier's Binary Chessboard Calculator - Subtraction

How to subtract one positive integer (the subtrahend) from another, larger positive integer (the minuend) (Gardner 1973):

Step 1.  Place the larger number on the bottom horizontal row.

Step 2.  Place the binary complement of the number to be subtracted in the margin below the bottom horizontal row. That is, where there would be a counter in the number itself, leave the square empty; and where there would not be a counter, place one on the square. Do this for all entries from right to left through the highest power of 2 occurring in the decomposition of the larger number.

Step 3.  Combine all the counters on the bottom horizontal row.

Step 4.  Abbreviate the board from right to left; that is, remove every two counters in a square and place one counter in the square to its left. This process often causes a "chain reaction" that "carries" into other squares, requiring further abbreviation.

Step 5.  Add one more counter in the 1's place (\(2^0\)-place) square in the bottom row. This may cause a "chain reaction" that "carries" into squares to the left, requiring further abbreviation.

Step 6.  The desired answer can now be obtained by converting the abbreviated difference back to a decimal number, except that you must ignore the farthest left counter (which may already have "fallen" off the left side of the board).

Example: That 116 – 84 = 32 is illustrated below.

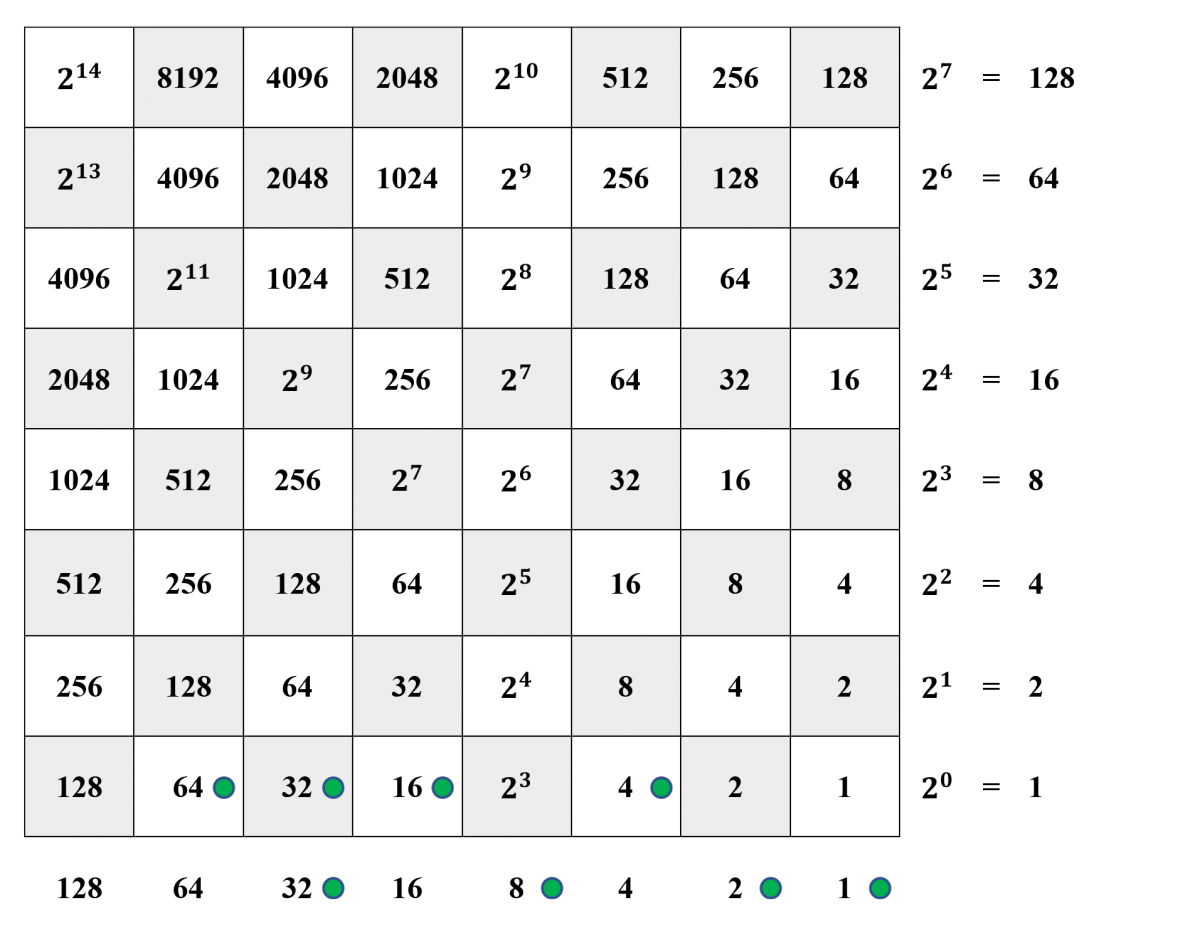
Steps 1 and 2. The larger integer, 116, decomposed as \[116 = 2^6 + 2^5 + 2^4 +{\phantom{2^3}}+2^2+{\phantom{2^1}}+{\phantom{2^0}} = 64 + 32 + 16 +{\phantom{8}}+4+{\phantom{2}}+{\phantom{1}},\] is represented by counters in the bottom horizontal row. Now we decompose 84 as \[\phantom{0}84 = 2^6 + {\phantom{2^5}}+ 2^4 +{\phantom{2^3}}+2^2+{\phantom{2^1}}+{\phantom{2^0}} = 64 +{\phantom{32}}+ 16 +{\phantom{8}}+4+{\phantom{2}}+{\phantom{1}},\] and write its complement \[{\phantom{84=2^6++}} {2^5} + {\phantom{2^4}} +{2^3}+{\phantom{2^2}} +{2^1}+{2^0}={\phantom{x2^6+}} 32 + {\phantom{16}} +8+{\phantom{4}} +2+1.\] The complement is represented in the margin below the bottom horizontal row.

The binary complement of a positive integer is sometimes called the "1's complement" because one can compute it by interchanging 0's and 1's in the binary-digit representation of the positive integer. For instance:

64        32        16         8         4         2         1

  1          0          1         0         1         0         0     \(\leftarrow\) Binary-digit representation for 84

  0          1          0         1         0         1         1     \(\leftarrow\) 1's complement of 84

The binary complement of 84 is therefore 32 + 8 + 2 + 1.

Step 3. Combine all of the counters in the bottom horizontal row:

Step 4. Abbreviate the row from right to left. Note that there is now a counter in the 128 or \(2^7\) place:

Step 5.  Add +1; that is, add one more counter to the 1's place, and ...

... abbreviate the row from right to left:

Step 6.  Now, ignoring the farthest left counter, the difference can be read from this row as 116 – 84 = 32.

Next: multiplication on the chessboard calculator