The Mathematical Cultures of Medieval Europe - Mathematics in Catholic Europe

It was, in fact, the existence of universities in Catholic Europe, beginning in the twelfth century, along with the concurrent flood of translations from the Arabic, that provided the impetus for the study and practice of mathematics (and other sciences) in Europe from that time on. However, the first important mathematician in Catholic Europe was Leonardo of Pisa (Fibonacci) (1170-1240), who was not connected to a university. He introduced parts of Islamic mathematics to Europe, after he had accompanied his merchant father on trips to North Africa and elsewhere in the Mediterranean, where he studied with Muslim mathematicians. He mastered the Hindu-Arabic number system as well as the elements of algebra, geometry, and trigonometry. So, in his first book, the Liber Abbaci of 1202, he spent many chapters describing computational methods and then another several chapters showing how to solve numerous types of problems. His methods of solution were varied, including the well-established method of the "rule of three." But since he had learned some algebraic methods as well, he sometimes included these. One of the standard types of problems solved by the rule of three was the “tree problem,” a problem to which he later reduced other types of problems:

There is a tree 1/4 + 1/3 of which lies underground, and it is 21 palms. It is sought what is the length of the tree. Because the least common denominator of 1/4 and 1/3 is 12, you see that the tree is divisible into 12 equal parts. Three plus four parts are 7 parts, and 21 palms; therefore, as the 7 is to the 21, so proportionally the 12 is to the length of the tree. And because the four numbers are proportional, the product of the first times the fourth is equal to the second by the third. Therefore, if you multiply the second 21 times the third 12, and you divide by the first number, namely by the 7, then the quotient will be 36 for the fourth unknown number, namely for the length of the tree; or because the 21 is triple the 7, you have triple the 12, and will have similarly 36. [Katz et al, 2016, 80]

Another standard problem that we have already seen abstractly in the work of Levi ben Gershon, is the problem of men finding a purse:

Two men who had denari found a purse with denari in it; thus found, the first man said to the second, If I take these denari of the purse, then with the denari I have, I shall have three times as many as you have. Alternately, the other man responded, And if I shall have the denari of the purse with my denari, then I shall have four times as many as you have. It is sought how many denari each has, and how many denari they found in the purse. [Katz et al, 2016, 81]

Interestingly, Leonardo did not mention that the problem is indeterminate; he just showed how to find one solution.

Besides these recreational problems, Leonardo devoted many pages to very practical problems such as calculation of profits, currency conversions, alloying of money, barter, determining values of merchandise, and so on. Given that his father was a merchant and that he lived in an Italy where commerce was quickly developing, it is not surprising that these kinds of problems would be of great interest to his readers. Although many of the problems are solved by seemingly ad hoc methods, Leonardo devoted a chapter to explaining the method of false position. Leonardo credited the method to the Arabs, and, of course, this method is found in Arabic texts written in North Africa, such as the work of ibn al-Banna’. This kind of problem is also found in Hebrew works. But Leonardo also devoted the concluding chapter of Liber abbaci to the Muslim method of solving quadratic equations, basically the work due to al-Khwārizmī. He then presented about 100 quadratic problems, taken from the works of such authors as al-Khwārizmī, Abū Kāmil, and al-Karajī.

In his Practical Geometry, Leonardo solved problems like those solved by ibn ‘Abdūn, ibn Ezra, and Abraham bar Ḥiyya. These are generally problems in measurement – of triangles, rectangles, squares, parallelograms, trapezoids, and parts of circles. Just like the earlier authors, sometimes he needed to solve quadratic equations to complete the solutions. From the similarity of some of his problems to those of bar Ḥiyya, in particular, it has been surmised that he had carefully read bar Ḥiyya’s text in its Latin translation.  But it should be noted that Fibonacci did not merely “copy” problems from earlier authors. He may well have read these authors, but he used his own genius to expand on their methods and often to figure out new and ingenious solutions. Thus, he presented a long series of problems on dividing a region into two equal parts. Some of these methods presumably come from the no-longer extant work of Euclid, and some of the methods are found in the work of bar Ḥiyya. But he very carefully explained his procedures and gave careful proofs.

Fibonacci also displayed a talent for abstract mathematics, demonstrated in his Book of Squares, initially prompted by a question from Master John of Palermo to “find a square number from which when five is added or subtracted always arises a square number.” He solved this problem and various associated problems through a series of 24 theorems, all given careful and detailed proofs [Leonardo, 1987]. So, it is clear that Leonardo felt that there was a readership for non-practical problems.

Leonardo was not connected to a university, unlike most of the mathematicians of medieval Europe who followed him. Thus, a few words about the universities are in order here. Well before the end of the twelfth century the Masters at the School of Saint Victor, together with the Masters at the Schools of St. Geneviève and Notre-Dame de Paris, would construct the cradle of the University of Paris. Oxford arose from dissatisfied, mostly English, Masters and students who left Paris for their homeland; similarly, Cambridge was founded from Oxford. The origins of universities in other countries have their own histories, such as the earlier University of Bologna, formed by the students who hired the Masters. The University of Montpellier, among several others, was founded in the thirteenth century. Some schools followed the English model with Masters in charge. Others followed the Italian model with students in charge. Regardless, if there be universities, there must be students, Masters, and a curriculum.

The new curriculum was the gift of the translators, operating mostly in Spain. The curriculum in arts at all the universities was based on the ancient trivium of logic, grammar, and rhetoric and the quadrivium of arithmetic, geometry, music, and astronomy. This study in the faculty of arts provided the student with preparation for the higher faculties of law, medicine, or theology. The centerpiece of the arts curriculum was the study of logic, and the primary texts for this were the logical works of Aristotle, all of which had recently been translated into Latin. The masters felt that logic was the appropriate first area of study since it taught the methods for all philosophic and scientific inquiry. Gradually, other works of Aristotle were also added to the curriculum.  For several centuries, the great philosopher’s works were the prime focus of the entire arts curriculum. Other authors were studied insofar as they allowed one better to understand this most prolific of the Greek philosophers. In particular, mathematics was studied in the universities primarily as it related to the work of Aristotle in logic or the physical sciences. (Algebra, on the other hand, was a non-university subject.) The mathematical curriculum itself – the quadrivium – usually consisted of arithmetic, taken from such works as Boethius’s adaptation of Nicomachus’s Introduction to Arithmetic or a medieval text on rules for calculation; geometry, taken from Euclid and one of the practical geometries; music, taken also from a work of Boethius; and astronomy, taken from Ptolemy’s Almagest and some more recent Latin translations of Islamic astronomical works.

What is important to realize is that, because the universities were corporate bodies generally operating under a royal charter, they were independent of church control. Now, Aristotle’s philosophy did pose problems for Catholic theologians. From Aristotle’s point of view, the world was eternal – it had always existed and would continue to exist. But for Catholics, as for Muslims and Jews, the world had been created by God out of nothing. In fact, in 1277, the Bishop of Paris drew up a list of 219 “errors” in which he alleged that “some scholars of arts at Paris” were transgressing the limits of their own faculty. In particular, he wrote that it was an error to doubt God’s omnipotence; that, in fact, God had absolute power to do whatever He wills, including creating the world out of nothing. Thus, he condemned those ideas that could not be maintained in light of the revealed truth of the Catholic religion.

But this condemnation was too little and too late. The religious elite who dominated intellectual thought had already concluded that rational thought and an empirical methodology were the tools for understanding the world.  In fact, a new canon law had been developed in the twelfth century stating that “anyone (and not just priests) ought to learn profane knowledge not just for pleasure but for instruction, in order that what is found therein may be turned to the use of sacred learning.” [Huff, 1993, 195] In essence, the study of the natural sciences and the pursuit of philosophical truth had become institutionalized in the universities and nothing would disturb this state of affairs. Scientists in Catholic Europe, including mathematicians, were free to study what they wished.

One group of mathematicians who worked at a university were the so-called Oxford calculators, associated with Merton College, Oxford during the fourteenth century. Because they were involved in university teaching, they had to figure out how to explain difficult concepts to students, with the basic method of teaching being disputations with participation from both Masters and students. Thus, they concentrated on logical argument, based on Aristotle’s principles, and then used the argument to try to determine what Aristotle meant in his discussions of physical problems. One of the first of the Mertonians was Thomas Bradwardine (1290-1349).

In his On the Continuum he mentioned five different opinions presented by scholars of his time and earlier:

One must know that the old and modern philosophers have five famous opinions about the composition of the continuum. Some of them, such as Aristotle, Averroes, Algazel [al-Ghazalī] and most of the moderns, argue that the continuum is not composed of atoms, but of parts that can be divided without end. Others say that it is composed of two kinds of indivisibles, because Democritus had assumed that the continuum consists of indivisible bodies. Others say that it consists of points, and this [assumption is divided] into two parts: Pythagoras (the father of this position), Plato, and our contemporary Walter [Chatton] assume that it is composed of a finite number of indivisibles, but others say that [it is composed] of an infinite number. This group, too, is divided into two parts. Some such as our contemporary Henry of Harclay say that it is composed of an infinite number of indivisibles that are directly joined. But others such as Lincoln [Robert Grosseteste], say [that it is composed] of an infinite number [of indivisibles] that are indirectly joined to one another. Therefore, the conclusion is this: “If one continuum is composed of indivisibles in some way” (the “way” includes any of the precedent ways), it then follows that “any continuum is composed of indivisibles according to a similar way.” [Katz et al, 2016, 178-179]

Bradwardine then presented arguments to reject most of these possibilities. For example, to reject the assumption that the continuum is composed of a finite number of points, he proved:

If this [is true], then the circumference of a circle is double of its diameter. This is: half of the circumference is equal to its diameter. From the different points of the diameter, [assuming that] they are 10, ten perpendiculars are drawn directly to different points on half the circumference. It follows that there are 10 points on half the circumference, because only one point on half the circumference corresponds [to] a perpendicular. Therefore equally, there are the same number of points on half the circumference as are on the diameter. Therefore, according to the second conclusion, half the circumference equals the diameter. [Katz et al, 2016, 179]

Bradwardine realized that this is impossible. Later, he rejected the hypothesis that a continuum is composed of an infinite number of indivisibles:

If this is true, a terminated surface can exceed another surface equal to it by any finite proportion. Let AB and CD be parallel lines. Atop base CE a right-angled parallelogram AFCE is constituted, and atop the same base another parallelogram CGHE is constituted with sides that are as much longer as you want than the sides of the parallelogram AFCE. [See Figure 8.] Then all lines of CGHE which are drawn from all points of CE to the opposite points of GH are equal in number to those points, and consequently to all perpendiculars of AFCE which are drawn from the same points to the opposite points. But they are longer than those [lines]. Therefore, CGHE is larger than AFCE. But according to I 36 of Euclid’s Elements, the parallelograms are equal. [Katz et al, 2016, 180]

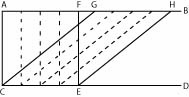
Figure 8. Bradwardine's parallelograms

Bradwardine finally announced his true view of the composition of continua:

No continuum is made up of atoms. From here follows and elicits: Every continuum is composed of an infinite number of continua of the same species as it, […] that is, every line is composed of an infinite number of lines, every surface composed of an infinite number of surfaces, and so on concerning other continua [Katz et al, 2016, 180].

Similarly, Bradwardine investigated four differing theories regarding relationships among speed (V), force (F), and resistance (R) in his Treatise on Proportions. First, he explained and demolished the thinking of Aristotle in On the Heavens and Earth: The proportion between the speeds with which motions take place varies as the difference whereby the power of the mover exceeds the resistance offered by the thing moved. Then he explained and rejected Averroes’ Comment 36 on Aristotle’s Physics Book VI: The proportion of the speeds of motions varies in accordance with the proportion of the excesses whereby the moving powers exceed the resisting powers. Next, he destroyed a generalization built on remarks in Aristotle’s Physics and On the Heavens and from On Weights: With the moving power remaining constant, the proportion of the speeds of motions varies in accordance with the proportion of resistances, and with the resistance remaining constant, it varies in accordance with the proportion of moving powers. Finally, he took apart Comment 79 on Aristotle’s Physics VIII by Averroes: There is neither any proportion nor any relation of excess between motive and resistive powers. Then he began his own contribution.

Now that these fogs of ignorance, these winds of demonstration, have been put to flight, it remains for the light of knowledge and of truth to shine forth. For true knowledge proposes a fifth theory, which states that the proportion of the speeds of motions varies in accordance with the proportion of the power of the mover to the power of the thing moved . . . Furthermore, there does not seem to be any theory whereby the proportion of the speeds of motions may be rationally defended, unless it is one of those already mentioned. Since, however, the first four have been discredited; therefore, the fifth must be the true one. We therefore arrive at the following theorem:

Theorem I. The proportion of the speeds of motions follows the proportion of the force of the mover to that of the moved, and conversely. Or, to put it another way, which means the same thing: The proportion of motive to resistive power is equal to the proportion of their respective speeds of motion, and conversely. This is to be understood in the sense of geometric proportionality. [Katz et al, 2016, 189-190]

Symbolically then, the first theorem can be expressed as \(V={\log}_n(F/R)\) or as \(n^V =F/R.\) That is to say, doubling the velocity squares the ratio of motive power to resistance, tripling the one cubes the other, and so on. For the formula to be correct universally, \(n\) is necessarily a constant equal to \(F/R\) when \(V = 1.\) Although the result is not our modern relationship, Bradwardine was able to use mathematical principles to prove various theorems dependent on his result.

An obvious question here is why, since Aristotle was important both to Muslim scientists, in the translation and adaptation of Averroes, and to Jewish mathematicians, in the Hebrew translations of Averroes, these men never considered the mathematical problems connected with kinematics. Perhaps in both cases these ideas would not be considered important enough religiously to be studied. But more certainly, the ideas of Aristotle were never discussed in a setting in which one could debate these questions. It seems clear from Bradwardine’s style, that it was through disputations that he could demolish certain arguments and therefore come up with one he believed correct.

Another prominent member of the Mertonian school was William Heytesbury (1313-1373). Continuing further the discussion of velocity, he was one of the first to state the Mean Speed Theorem: A body that moves with uniformly accelerating speed traverses in a given time the same distance as a body that in the same time moves with a constant speed equal to the accelerating body’s speed at the middle instant. Heytesbury gave a demonstration of this result by an argument from symmetry, and then proved the easy corollary, that under uniformly accelerated motion from rest, a body in the first half of a given interval will traverse one-third of the distance it covers in the second half of the interval.

Heytesbury’s slightly younger contemporary Nicole Oresme (1320-1382), connected with the University of Paris, made some further advances by using a graphing technique to visualize continuous quantity. As he put it,

[E]very intensity which can be acquired successively ought to be imagined by a straight line perpendicularly erected on some point of the space or subject of the intensible thing, e.g., a quality. For whatever ratio is found to exist between intensity and intensity, in relating intensities of the same kind, a similar ratio is found to exist between line and line, and vice versa. [Katz et al, 2016, 197]

Oresme applied his result to all sorts of “intensities” and drew figures to represent uniform qualities, uniformly difform qualities as well as difformly difform qualities:

[E]very uniform quality is imagined by a rectangle and every quality uniformly difform terminated at zero degree is imaginable by a right triangle. Further, every quality uniformly difform terminated in both extremes at some degree is to be imagined by a quadrangle having right angles on its base and the other two angles unequal. Now every other linear quality is said to be “difformly difform” and imaginable by means of figures otherwise disposed according to manifold variation. [Katz et al, 2016, 199]

This geometric representation enabled Oresme to give a simple geometric proof of the Mean Speed theorem. However, he was a bit puzzled when he tried to apply his methodology to the idea of curvature, because he could not figure out how to compare different curvatures.

For curvature, like the other qualities, has both extension and intensity, and one kind of curvature is uniform while another is difform. But still it is not manifest, in regard to the ratio of the intensity of curvatures, whether one is double another or exists in another ratio to it, or whether or not curvatures are unrelatable one to the other by ratio. [Clagett, 1968, 215]

Oresme wanted to define increase in curvature as a function of “its departure from straightness,” but could not actually measure this. He could certainly tell if one curve was more “curved” than another by looking at whether one could be included in the space between the second and a straight line – but this now involved the whole notion of the angle of contingence, that is, the angle between a circle and its tangent, and it was reasonably clear, even to Oresme, that measurement of these “quantities” was not possible. On the other hand, Oresme noted that “every circular curvature is uniform and vice versa, and every other curvature is difform.” He could measure circular curvature:

Its intensity is measured by the quantity of the radius of the circle whose curve is … the circumference, so that by the amount the radius is less, so proportionally the curvature will be greater [Clagett, 1968, 221].

This was quite an insight for the fourteenth century. However, Oresme was less successful when he tried a counting argument for figuring out the total number of combinations of six simple types of figures representing quality. Although Hebrew writers before Oresme, including both ibn Ezra and Levi ben Gershon, had shown how to calculate such values, Oresme somehow made an error. In fact, combinatorial reasoning was not to be fully developed in Europe for another two hundred years.

While mathematics at the universities was clearly important, with the practitioners delving into philosophical questions coming out of Aristotle, the growth of commerce in Italy beginning in the thirteenth century spawned a different kind of mathematics. The Italian merchants of the Middle Ages generally were what today we might call venture capitalists. They traveled themselves to distant places in the East, bought goods which were wanted back home, then returned to Italy to sell them in the hope of making a profit. These traveling merchants needed very little mathematics other than the ability to determine their costs and revenues for each voyage. By the early fourteenth century, however, a commercial revolution spurred originally by the demands of the Crusades had begun to change this system greatly. New technologies in shipbuilding and greater safety on the shipping lanes helped to replace the traveling merchants of the Middle Ages with the sedentary merchants of the Renaissance. These “new men” could remain at home in Italy and hire others to travel to the various ports, make the deals, act as agents, and arrange for shipping. Thus, international trading companies began to develop in the major Italian cities, companies that had a need for more sophisticated mathematics than did their predecessors. These new companies had to deal with letters of credit, bills of exchange, promissory notes, and interest calculations. Business was no longer composed of single ventures but of a continuous flow of goods consisting of many shipments from many different ports enroute simultaneously. The medieval economy, based in large part on barter, was gradually being replaced by a money economy.

The Italian merchants needed a new facility in mathematics to be able to deal with the new economic circumstances, but the mathematics they needed was not the mathematics of the quadrivium, the mathematics studied in the universities. They needed new tools for calculating and problem solving. To meet this need, a new class of “professional” mathematicians, the maestri d’abbaco or abacists, appeared in early fourteenth century Italy. These professionals wrote the texts from which they taught the necessary mathematics to the sons of the merchants in new schools created for this purpose.

In addition to the algorithms of the Hindu-Arabic number system, the abacists taught their students methods of problem solving using the tools of both arithmetic and Islamic algebra. The texts written by the abacists, of which several hundred different ones still exist, are generally large compilations of problems along with their solutions. These include not only genuine business problems of the type the students would have to solve when they joined their fathers’ companies, but also plenty of recreational problems typical of the kind found in modern elementary algebra texts. There were also sometimes geometrical problems as well as problems dealing with elementary number theory, the calendar, and astrology.  The solutions in the texts were written in great detail with every step fully described, but, in general, no reasons were given for the various steps. Perhaps the teachers did not want to disclose their methods in written form, fearing that then there would no longer be any reason to hire them.  In any case, it seems clear that these abacus texts were designed not only for classroom use, but also to serve as reference manuals for the merchants themselves. A merchant could easily find and readily follow the solution of a particular type of problem without the necessity of understanding the theory.

Among the many extant abacist texts, we consider just the Libro di Ragioni by Paoli Girardi, written in Montpellier in 1327. Of course, Montpellier was not only a university town, but also a center for trade in the south of France. Although Paoli was from Florence, it is therefore not surprising that he travelled to Montpellier.  His text contained not only the basic rules common to such texts, but also some theoretical explanations of rules for solving equations, including the basic al-Khwārizmī rules for quadratics. He tried to appeal to his students by writing the problems as practical ones:

A man loaned 20 lire to another for two years at compound interest. When the end of 2 years came he gave me 30 lire. I ask you at what rate was the lire loaned per month?

There is a man who went on 2 voyages. On the first voyage, he earned 12 denari. On the second voyage, he earned at the same rate that he made on the first voyage, and at the end he found [he had] 100 denari. I ask you with how many denari did he leave?

Interestingly, Paolo did not write his problems so they would have simple whole number answers. The answer to the first problem was that the lire were loaned at the rate of the root of 600 minus 20 denari per month. The answer to the second problem was that the merchant began with the root of 1300 plus 38 denari.

For another example of a 14th century abacist text, see "Mathematical Treasure: Problems from the Zibaldone da Canal."